Площа рівнобедреного трикутника

У даному уроці розміщені формули і задачі на знаходження площі рівнобедреного трикутника. Формули забезпечені поясненнями і коментарями. На окремому рисунку наведено відповідність умовних позначень формул і елементів рівнобедреного трикутника. Далі наведено розділ з прикладами розв'язання задач.

См. також:

Обозначения в равнобедренном треугольнике, которые используются в формулах. Позначення в рівнобедреному трикутнику, які використовуються у формулах.

Літерні позначення сторін і кутів на рисунку відповідають позначенням, що вказані у формулах. Таким чином, це допоможе Вам зіставити їх з елементами рівнобедреного трикутника. З умов задачі визначте, які елементи відомі, знайдіть на кресленні їх позначення і підберіть підходящу формулу.

Формула площі рівнобедреного трикутника

Формулы нахождения площади равнобедренного треугольника через его стороны и углы, а также через основание и высоту

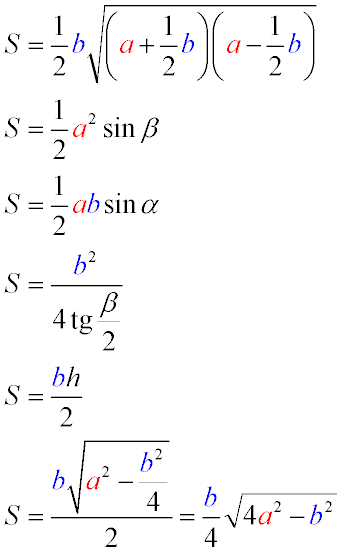
Далi наведені формули знаходження площі рівнобедреного трикутника: сторони, бічні сторони і кут між ними, через бічну сторону, підстава і кут при вершині, через сторону основи і кут при основі і т. д. Просто знайдіть найбільш підходящу на малюнку зліва. Для найдопитливіших в тексті праворуч пояснюється, чому формула явяляется правильної і саме з її допомогою знаходиться площа.

Площа рівнобедреного трикутника можна знайти, знаючи його бік і основання. Цей вираз було отримано шляхом спрощення більш загальної, універсальної формули. Якщо взяти за основу формулу Герона, а потім взяти під увагу, що дві сторони трикутника рівні між собою, то вираз спрощується до формули, представленої на зображенні.
Приклад використання такої формули наведено на прикладі розв'язання задачі нижче.
Друга формула дозволяє знайти його площу через бічні сторони і кут між ними - це половина квадрата бічної сторони, помножена на синус кута між бічними сторонами
Якщо подумки опустити висоту на бічну сторону рівнобедреного трикутника, зауважимо, що її довжина дорівнюватиме a * sin β. Оскільки довжина бічної сторони нам відома, висота, опущена на неї тепер відома, половина їх твори та буде дорівнює площі даного рівнобедреного трикутника (Пояснення: повне твір дає площа прямокутника, що очевидно. Висота ділить цей прямокутник на два малих прямокутника, при цьому сторони трикутника є їх діагоналями, які ділять їх рівно навпіл. Таким чином, площа рівнобедреного трикутника і буде дорівнює половині добутку бічної сторони на висоту). См. також Формулу 5
Третя формула показує знаходження площі через бічну сторону, основу і кут при вершині.
Строго кажучи, знаючи один з кутів рівнобедреного трикутника, можна знайти й інші, тому застосування даної або попередньої формули - питання смаку (до речі, тому можна запам'ятати тільки одну з них).
У третьої формули також є ще одна цікава особливість - твір a sin α дасть нам довжину висоти, опущеної на основу. В результаті ми отримаємо просту і очевидну формулу 5.
Площа рівнобедреного трикутника можна також знайти через сторону основи і кут при основі (кути при підставі рівні) як квадрат підстави, поділений на чотири тангенса половини кута, утвореного його бічними сторонами. Якщо придивитися уважніше, то стане очевидно, що половина підстави (b/2) помножена на tg(β/2) дасть нам висоту трикутника. Оскільки висота в равнобедренном трикутнику є, одночасно, бісектрисою і медіаною, то tg(β/2) - це відношення половини підстави (b/2) до висоті - tg(β/2) = (b/2)/h. Звідки h = b / (2 tg(β/2) ). У результаті формула знову буде зведена до більш простою Формулою 5, яка цілком очевидна.
Зрозуміло, площу рівнобедреного трикутника можна знайти, опустивши висоту з вершини на основу, в результаті чого вийде два прямокутних трикутника. Далі - все очевидно. Половина твору висоти на основу і є шукана площа. Приклад використання даній формулі, див. задачі нижче (2-й спосіб рішення)
Ця формула виходить, якщо спробувати знайти площу рівнобедреного трикутника за допомогою теореми Піфагора. Для цього виразимо висоту з попередньої формули, яка одночасно є катетом прямокутного трикутника, утвореного бічною стороною, половиною його заснування і висотою, через теорему Піфагора. Бічна сторона є гіпотенузою, тому з бічної сторони квадрата (а) віднімемо квадрат другого катета. Оскільки він дорівнює половині підстави (b/2) то його квадрат буде дорівнює b²/4. Знаходження кореня з даного виразу і дасть нам висоту. Що і видно в Формулі 6. Якщо чисельник і знаменник помножити на два, а потім двійку чисельника внести під знак кореня, отримаємо другий варіант тієї ж самої формули, який написаний через знак "дорівнює".
До речі, найкмітливіші можуть побачити, що якщо в Формулі 1 розкрити дужки, то вона перетворитися в Формулу 6. Або навпаки, різниця квадратів двох чисел, розкладена на множники, дасть нам вихідну, першу.

Позначення, які були застосовані у формулах на рисунку:

a - довжина однієї з двох рівних сторін трикутника

b - довжина основи

α - величина одного з двох рівних кутів при основі

β - величина кута між рівними сторонами трикутника і противолежащего його основи

h - довжина висоти, опущена з вершини на основу рівнобедреного трикутника

Важливо. Зверніть увагу на позначення змінних! Не переплутайте α і β, а також a і b!

См. також: інші формули і властивості рівнобедреного трикутника

Примітка. Це частина уроку із завданнями з геометрії (розділ площа рівнобедреного трикутника). Тут розміщені завдання, які викликають труднощі при рішенні. Якщо Вам необхідно вирішити завдання з геометрії, якої тут немає - пишіть про це у форумі. Для позначення дії витягу квадратного кореня в рішеннях задач використовується символ √ або sqrt(), при чому в дужках вказано підкореневий вираз.

Завдання

Бічна сторона рівнобедреного трикутника дорівнює 13 см, а основа дорівнює 10 див. Знайдіть площу рівнобедреного трикутника.

Равнобедренный треугольник с биссектрисой от бокового угла

Рішення.

1-й спосіб. Застосуємо формулу Герона. Оскільки трикутник рівнобедрений, то вона прийме більш простий вигляд (див. формулу 1 в списку формул вище):
Площа рівнобедреного трикутника

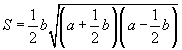
де а - довжина бічних сторін, а b - довжина основи.
Підставивши значення довжин сторін трикутника з задачі, отримаємо:
S = 1/2 * 10 * √ ((13 + 5 )( 13 - 5 )) = 5 √ (18 * 8) = 60 см²

2-й спосіб. Застосуємо теорему Піфагора
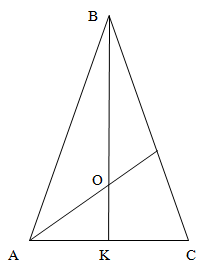
Припустимо, що ми не пам'ятаємо формулу, використану в першому способі рішення. Тому опустимо з вершини B на підставу AC висоту BK.
Оскільки висота рівнобедреного трикутника ділить його основу навпіл, то довжина половини підстави буде дорівнює
AK = AC / 2 = 10 / 2 = 5 см .

Висота з половиною підстави і стороною рівнобедреного трикутника утворює прямокутний трикутник ABK. У цьому трикутнику нам відома гіпотенуза AB і катет AK. Виразимо довжину другого катета через теорему Піфагора.

Відповідно, висота буде дорівнює:

h = √ ( 13² - 5² ) = √144 = 12 см

Площа вихідного рівнобедреного трикутника ABC дорівнює площі двох прямокутних трикутників ABK і CBK, утворених бічними сторонами, висотою і половинами підстави рівнобедреного трикутника. Обидва прямокутних трикутника рівні між собою. Гіпотенузи - це сторони рівнобедреного трикутника, тому вони рівні, один із катетів - загальний, а, оскільки, BK одночасно є і бісектрисою і висотою, то, відповідні кути також рівні. Тому нам буде досить знайти площу одного з них і помножити отримане число на два.

Застосувавши формулу площі прямокутного трикутника, отримаємо:

S = AK * BK / 2
S = 5 * 12 / 2 = 30 см²

Оскільки у складі трикутника ABC два рівних прямокутних трикутника ABK і CBK, то загальна площа рівнобедреного трикутника ABC складе:

30 * 2 = 60 см² .

Як видно, обидва способи рішення дають один і той же результат.

Відповідь: Площа рівнобедреного трикутника становить 60 см2 .

Рiвнобедрений трикутник | Описание курса | Прямокутний трикутник