Таблиця значень тригонометричних функцій

Примітка. В даній таблиці значень тригонометричних функцій використовується знак √ для позначення квадратного кореня. Для позначення дробу - символ "/".

Див. також корисні матеріали:

• Формули перетворення тригонометричних функцій 
• Таблиця похідних тригонометричних функцій 
• Як обчислені ці значення 

Для визначення значення тригонометричної функції, знайдіть його на перетині рядка з зазначенням тригонометричної функції. Наприклад, синус 30 градусів - шукаємо колонку з заголовком sin (синус) і знаходимо перетин цієї колонки таблиці з рядком "30 градусів", на їх перетині зчитуємо результат - одна друга. Аналогічно знаходимо косинус 60 градусів, синус 60 градусів (ще раз, в перетині колонки sin (синус) і рядки 60 градусів знаходимо значення sin 60 = √3 / 2) і т.д. Точно так же знаходяться значення синусів, косинусів і тангенсів інших "популярних" кутів.

Синус пі, косинус пі, тангенс пі і інших кутів в радіанах

Наведена нижче таблиця косинусів, синусів і тангенсів також підходить для знаходження значення тригонометричних функцій, аргумент яких заданий в радіанах. Для цього скористайтеся другий колонкою значень кута. Завдяки цьому можна перевести значення популярних кутів з градусів в радіани. Наприклад, знайдемо кут 60 градусів в першому рядку і під ним прочитаємо його значення в радіанах. 60 градусів одно π / 3 радіан.

Число пі однозначно висловлює залежність довжини кола від градусної міри кута. Таким чином, пі радіан рівні 180 градусам. 

Будь-яке число, виражене через пі (радіан) можна легко перевести в градусну міру, замінивши число пі (π) на 180.

Приклади: 

1. Синус пі.
sin π = sin 180 = 0
таким чином, синус пі - це те ж саме, що синус 180 градусів і він дорівнює нулю.

2. Косинус пі.
cos π = cos 180 = -1
таким чином, косинус пі - це те ж саме, що косинус 180 градусів і він дорівнює мінус одиниці.

3. Тангенс пі
tg π = tg 180 = 0
таким чином, тангенс пі - це те ж саме, що тангенс 180 градусів і він дорівнює нулю.

Таблиця значень синуса, косинуса, тангенса для кутів 0 - 360 градусів (значення, якi часто зустрічаються )   

значення кута α (градусів)	значення кута α в радіанах (Через число пі)	sin  (синус)	cos  (косинус)	tg  (тангенс)	ctg  (котангенс)	sec  (секанс)	cosec  (косеканс)
0	0	0	1	0	-	1	-
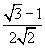
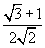
15	π/12			2 - √3	2 + √3
30	π/6	1/2	√3/2	1/√3	√3	2/√3	2
45	π/4	√2/2	√2/2	1	1	√2	√2
60	π/3	√3/2	1/2	√3	1/√3	2	2/√3
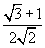
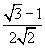
75	5π/12			2 + √3	2 - √3
90	π/2	1	0	-	0	-	1
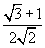
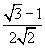
105	7π/12		-	- 2 - √3	√3 - 2
120	2π/3	√3/2	-1/2	-√3	-√3/3
135	3π/4	√2/2	-√2/2	-1	-1	-√2	√2
150	5π/6	1/2	-√3/2	-√3/3	-√3
180	π	0	-1	0	-	-1	-
210	7π/6	-1/2	-√3/2	√3/3	√3
240	4π/3	-√3/2	-1/2	√3	√3/3
270	3π/2	-1	0	-	0	-	-1
360	2π	0	1	0	-	1	-

Якщо в таблиці значень тригонометричних функцій замість значення функції вказано прочерк (тангенс (tg) 90 градусів, котангенс (ctg) 180 градусів) означає при даному значенні градусної міри кута функція не має певного значення. Якщо ж прочерку немає - клітина порожня, значить ми ще не внесли потрібне значення. Ми цікавимося, по яких запитах до нас приходять користувачі і доповнюємо таблицю новими значеннями, незважаючи на те, що поточних даних про значеннях косинусів, синусів і тангенсів найчастіших значень кутів цілком достатньо для вирішення більшості завдань. 

аблиця значень тригонометричних функцій sin, cos, tg для найбільш популярних кутів
0, 15, 30, 45, 60, 90 ... 360 градусів 
(Цифрові значення "як за таблицями Брадіса")  

значення кута α (граду сів )	значення кута α в радіанах	sin (синус)	cos (косинус)	tg (тангенс)	ctg (котангенс)
0	0	0	1	0	-
15	π/12	0,2588	0,9659	0,2679	3,7321
30	π/6	0,5000	0,8660	0,5774	1,7321
45	π/4	0,7071	0,7071	1	1
50	5π/18	0,7660	0,6428	1.1918	0,8391
60	π/3	0,8660	0,5000	1,7321	0,5774
65	13π/36	0,9063	0,4226	2,1445	0,4663
70	7π/18	0,9397	0,3420	2,7475	0,3640
75	5π/12	0,9659	0,2588	3,7321	0,2679
90	π/2	1	0	-	0
105	5π/12	0,9659	-0,2588	-3,7321	-0,2679
120	2π/3	0,8660	-0,5000	-1,7321	-0,5774
135	3π/4	0,7071	-0,7071	-1	-1
140	7π/9	0,6428	-0,7660	-0,8391	-1,1918
150	5π/6	0,5000	-0,8660	-0,5774	-1,7321
180	π	0	-1	0	-
270	3π/2	-1	0	-	0
360	2π	0	1	0	-

Іноді для швидких розрахунків потрібно не точне, а обчислюється значення (число десятковим дробом), яке раніше шукали в таблицях Брадіса. Тому, на додаток до таблиці точних значень тригонометричних функцій наведені ці ж самі значення, але у вигляді десяткового дробу, округленої до четвертого знака. Додатково в таблицю включені "нестандартні" значення тангенса, косинуса, синуса 140 градусів, синуса 105, 70, косинуса 105 і 50 градусів.

Приклад: синус 60 градусів дорівнює приблизно 0,866025404, а в таблиці вказано значення sin 60 ≈ 0,8660; косинус 30 градусів дорівнює цьому ж самому числу (див. формули перетворення тригонометричних функцій)