|
Теорема косінусів формулюється так: квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку
цих сторін на косинус кута між ними.
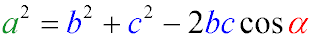
Завдання
Одна зі сторін трикутника більша за іншу на 8 сантиметрів, а кут між ними дорівнює 120 градусам. Знайдіть периметр трикутника,
якщо довжина третьої сторони дорівнює 28 см.
Рішення.
Позначимо одну із сторін трикутника як x, тоді величина іншої дорівнює x+8 см.
Виходячи з теореми косінусів, отримаємо:
282 = x2 + (x+8)2-2x(x+8)cos120o
784 = x2 + x2 +16x + 64 - 2x(x+8)(-0,5)
784 = 2x2+16x + 64 + x(x+8)
720 = 3x2 + 16x + 8x
3x2 + 24x +720 = 0
D=9216
x1=((-24)+96)/6=12 (другий корінь є негативним числом і не має сенсу в рамках розв'язання задачі)
Таким чином, периметр трикутника P=12+(12+8)+28 = 60 см.
Відповідь: 60 см
Завдання
У трикутнику АВС сторона АС дорівнює 7√3 см, сторона ВС дорівнює 1 см. Кут С дорівнює 150 градусів. Знайти довжину сторони АВ.
Рішення.
Застосуємо теорему косінусів та відповідну формулу (див. вище)
AB2 = (7√3)2 + 12 - 2 (7√3) cos 150º
Значення косинуса 150 градусів знайдемо за таблицею значень тригонометричних функцій.
AB2 = 147 + 1 - 14√3 (-√3/2)
AB2 = 148 + 21 = 169
AB = 13
Відповідь: 13 см
Теорема косинусів і її доказ |
Описание курса
| Тангенс та його властивості
|

