Примітка. У даному уроці викладено теоретичні матеріали і рішення завдань з геометрії на тему "медіана у прямокутному трикутнику".
Якщо Вам необхідно вирішити завдання з геометрії, якої тут немає - пишіть про це у форумі. Майже напевно курс буде доповнено.
См. также этот урок на русском языке.
Властивості медіани прямокутного трикутника
Визначення медiани
|
Медіаною трикутника називається відрізок, що з'єднує один з кутів трикутника з серединою протилежної йому сторони.
(медіаною також називають пряму, що містить даний відрізок)
|
- Медіани трикутника перетинаються в одній точці і діляться цією точкою на дві частини у відношенні 2:1, рахуючи від вершини кута. Точка їх перетину називається центром тяжіння трикутника (відносно рідко у завданнях для позначення цієї точки використовується термін "центроїд")
- Медіана розбиває трикутник на два рівновеликих трикутника
- Трикутник ділиться трьома медианами на шість рівновеликих трикутників
- Більшої сторони трикутника відповідає менша медіана.
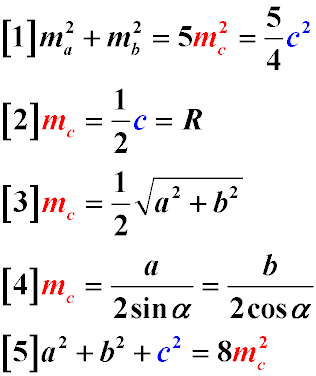
Задачі з геометрії, пропоновані для вирішення, в основному, використовують наступні властивості медіани прямокутного трикутника:
- Сума квадратів медіан, опущених на катети прямокутного трикутника дорівнює п'яти квадратах медіани, опущеною на гіпотенузу (формула 1)
- Медіана, опущена на гіпотенузу прямокутного трикутника дорівнює половині гіпотенузи (формула 2)
- Медіана, опущена на гіпотенузу прямокутного трикутника, дорівнює радіусу кола, описаного навколо прямокутного трикутника (формула 3)
- Медіана, опущена на гіпотенузу, дорівнює половині квадратного кореня з суми квадратів катетів (формула 4)
- Медіана, опущена на гіпотенузу, дорівнює частці від ділення довжини катета на два синуса противолежащего катету гострого кута (формула 5)
- Медіана, опущена на гіпотенузу, дорівнює частці від ділення довжини катета на два косинуса прилеглого катету гострого кута (формула 6)
- Сума квадратів сторін прямокутного трикутника дорівнює восьми квадратах медіани, опущеною на його гіпотенузу (формула 7)
Позначення в формулах:
a, b - катети прямокутного трикутника
c - гіпотенуза прямокутного трикутника
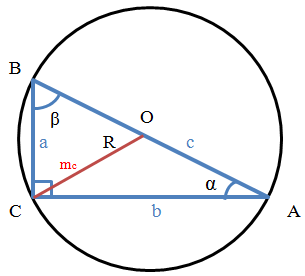
Якщо позначити трикутник, як ABC, то
ВС = а
AC = b
AB = c
(тобто сторони a,b,c - є протилежними відповідним кутам)
ma - медіана, проведена до катету а
mb - медіана, проведена до катету b
mc - медіана прямокутного трикутника, проведена до гіпотенузи с
α (альфа) - кут CAB, протилежний стороні а
Задача про медіану у прямокутному трикутнику
Медіани прямокутного трикутника, проведені до катетам, дорівнюють, відповідно, 3 см і 4 див. Знайдіть гіпотенузу трикутника.
Рішення.
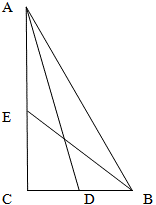
Перш ніж розпочати вирішення завдання, звернемо увагу на співвідношення довжини гіпотенузи прямокутного трикутника і медіани, яка опущена на неї. Для цього звернемося до формулами 2, 4, 5 властивостей медіани в прямокутному трикутнику. В цих формулах явно вказано співвідношення гіпотенузи і медіани, яка на неї опущена як 1 до 2. Тому,для зручності майбутніх обчислень (що ніяк не вплине на правильність рішення, але зробить його більш зручним), позначимо довжини катетів AC і BC через змінні x та y як 2x і 2y (а не x і y).
Розглянемо прямокутний трикутник ADC. Кут C у нього прямий за умовою задачі, катет AC - загальний з трикутником ABC, а катет CD дорівнює половині BC згідно властивостям медіани. Тоді, по теоремі Піфагора
AC2 + CD2 = AD2
Оскільки AC = 2x, CD = y (так як медіана ділить катет на дві рівні частини), то
4x2 + y2 = 9
Одночасно, розглянемо прямокутний трикутник EBC. У нього також кут З прямою за умовою задачі, катет BC є спільним з катетом BC вихідного трикутника ABC, а катет EC за властивістю медіани дорівнює половині катета AC вихідного трикутника ABC.
По теоремі Піфагора:
EC2 + BC2 = BE2
Оскільки EC = x (медіана ділить катет навпіл), BC = 2y, то
x2 + 4y2 = 16
Так як трикутники ABC, EBC і ADC пов'язані між собою загальними сторонами, то обидва отриманих рівняння також пов'язані між собою.
Розв'яжемо отриману систему рівнянь.
4x2 + y2 = 9
x2 + 4y2 = 16
Складемо обидва рівняння (втім, можна було вибрати і будь-який інший спосіб рішення).
5x2 + 5y2 = 25
5( x2 + y2 ) = 25
x2 + y2 = 5
Звернемося до вихідного трикутника ABC. За теоремою Піфагора
AC2 + BC2 = AB2
Так як довжина кожного з катетів нам "відома", ми прийняли, що їх довжина дорівнює 2x і 2y, тобто
4x2 + 4y2 = AB2
Так як обидва доданки мають спільний множник 4, винесемо його за дужки
4 ( x2 + y2 ) = AB2
Чому дорівнює x2 + y2 ми вже знаємо (див. вище x2 + y2 = 5), тому просто підставимо значення замість x2 + y2
AB2 = 4 х 5
AB2 = 20
AB = √20 = 2√5
Відповідь: довжина гіпотенузи дорівнює 2√5

