|
Див. також Теорема синусов.
Формулювання і доведення теореми косинусів
Теорема косинусів є узагальненням теореми Піфагора для довільного трикутника.
Формулювання теореми косинусів
Для плоского трикутника зі сторонами a, b, c і кутом α, протилежними стороні a, справедливо співвідношення:
|
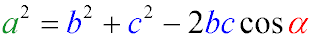
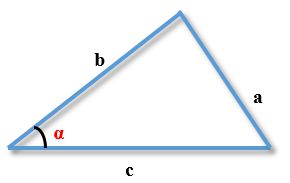
Квадрат одного боку трикутника дорівнює сумі квадратів двох інших сторін за вирахуванням подвоєного їх твору, помноженого на косинус кута між ними
|
Корисні формули теореми косинусів:
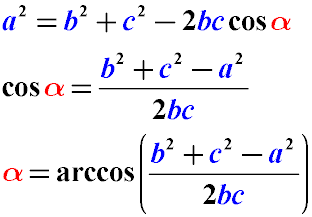
Як видно із зазначеного вище, за допомогою теореми косинусів можна знайти не тільки сторону трикутника за двома сторонами і кутом між ними, можна, знаючи розміри всіх сторін трикутника, визначити косинуси всіх кутів, а також обчислити величину будь-якого кута трикутника. Обчислення будь-якого кута трикутника по його сторонах є наслідком перетворення формули теореми косинусів.
Доказ теореми косинусів
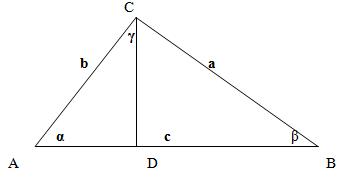
Розглянемо довільний трикутник ABC. Припустимо, що нам відома величина боку AC (вона дорівнює нікому числу b), величина боку AB (вона дорівнює нікому числу c) і кут між цими сторонами, величина якого дорівнює α. Знайдемо величину сторони BC (позначивши її довжину через змінну a)
Для доведення теореми косинусів проведемо додаткові побудови. З вершини C на сторону AB опустимо висоту CD.
Знайдемо довжину сторони AB. Як видно з малюнка, в результаті додаткового побудови можна сказати, що
AB = AD + BD
Знайдемо довжину відрізка AD. Виходячи з того, що трикутник ADC є прямокутним, нам відомі довжина його гіпотенузи (b) і кут (α) то величину сторони AD можна знайти із співвідношення його сторін, користуючись властивостями тригонометричних функцій в прямокутному трикутнику:
AD / AC = cos α
звідкі
AD = AC cos α
AD = b cos α
Довжину сторони BD знайдемо як різницю AB і AD:
BD = AB - AD
BD = c − b cos α
Тепер запишемо теорему Піфагора для двох прямокутних трикутників ADC і BDC:
для трикутника BDC
CD2 + BD2 = BC2
для трикутника ADC
CD2 + AD2 = AC2
Звернемо увагу на те, що обидва трикутника мають загальну сторону - CD. Визначимо її довжину для кожного трикутника - винесемо її значення в ліву частину виразу, а решта - в праву.
CD2 = BC2 - BD2
CD2 = AC2 - AD2
Оскільки ліві частини рівнянь (квадрат сторони CD) рівні, то прирівняємо праві частини рівнянь:
BC2 - BD2 = AC2 - AD2
Виходячи із зроблених раніше обчислень, ми вже знаємо що:
AD = b cos α
BD = c − b cos α
AC = b (за умовою)
А значення сторони BC позначимо як a.
BC = a
(Саме його нам і потрібно знайти)
Отримаємо:
BC2 - BD2 = AC2 - AD2
Замінимо буквені позначення сторін на результати наших обчислень
a2 - ( c − b cos α )2 = b2 - ( b cos α )2
перенесемо невідоме значення (а) на ліву сторону, а решта частини рівняння - на праву
a2 = ( c − b cos α )2 + b2 - ( b cos α )2
розкриємо дужки
a2 = b2 + c 2 - 2c b cos α + ( b cos α )2 - ( b cos α )2
отримуємо
a2 = b2 + c 2 - 2bc cos α
Теорема косинусів доведена.
Випадок, коли один з кутів при підставі тупий (і висота падає на продовження основи), повністю аналогічний розглянутому.
Косинус |
Описание курса
| Тригонометричне коло
|
