Рiвняння кола
Аналітична геометрія дає однакові прийоми розв'язування геометричних задач. Для цього всі задані й шукані точки і лінії відносять до однієї системи координат.
У системі координат можна кожну точку охарактеризувати її координатами, а кожну лінію - рівняння з двома невідомими, графіком якого ця лінія є. Таким чином, геометрична задача зводиться до алгебраїчної, де добре відпрацьовані всі прийоми обчислень.
Окружність є геометричне місце точок з одною певною властивістю (кожна точка окружності рівновіддалена від однієї точки, яка називається центром). Рівняння кола має відображати цю властивість задовольняти цій умові.
Геометрична інтерпретація рівняння кола - це лінія кола.
Якщо помістити окружність в систему координат, то всі точки кола відповідають одній умові - відстань від них до центру кола, має бути однаковою і належати колу.
Коло з центром у точці А і радіусом R помістимо в координатну площину.
Якщо координати центру (а;b), а координати будь-якої точки кола (х;у), то рівняння кола має вигляд:
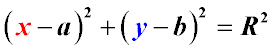
Якщо квадрат радіусу кола дорівнює сумі квадратів різниць відповідних координат будь-якої точки кола та її центру, то це рівняння є рівнянням кола у плоскій системі координат.
Якщо центр кола співпадає з точкою початку координат, то квадрат радіусу кола дорівнює сумі квадратів координат будь-якої точки кола. В цьому випадку рівняння окружності приймає вигляд:
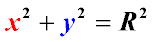
Отже, будь-яка геометрична фігура для якої геометричне місце точок визначається рівнянням, що зв'язує координати її точок. І навпаки, рівняння, що зв'язує координатиx і y, що визначають лінію як геометричне місце точок площини, координати яких задовольняють даному рівнянню.
Приклади розв'язання задач про рівняння кола
Завдання. Скласти рівняння заданої окружності
Складіть рівняння кола з центром в точці O (2; -3) і радіусом 4.
Рішення.
Звернемося до формули рівняння окружності:
R2 = (x - a)2 + (y - b)2
Підставимо значення в формулу.
Радіус кола R = 4
Координати центру кола (відповідно до умовою)
a = 2
b = -3
отримуємо:
(x - 2)2 + (y - (-3))2 = 42
або
(X - 2)2 + (y + 3)2 = 16.
Завдання. Чи належить точка рівняння окружності
Перевірити, чи належить точка A (2; 3) рівнянню кола (x - 2)2 + (y + 3)2 = 16.
Рішення.
Якщо точка належить колу, то її координати задовольняють рівнянню окружності.
Щоб перевірити, чи належить окружності точка з заданими координатами, підставимо координати точки в рівняння заданої окружності.
У рівняння (x - 2)2 + (y + 3)2 = 16
підставимо, згідно з умовою, координати точки А (2; 3), тобто
x = 2
y = 3
Перевіримо істинність отриманого рівності
(x - 2)2 + (y + 3)2 = 16
(2 - 2)2 + (3 + 3)2 = 16
0 + 36 = 16 рівність є невірною
Таким чином, задана точка не належить заданому рівнянню кола.
Площа геометричної фігури |
Описание курса
| Хорда
|

