Синус, косинус і тангенс кута 120 градусів

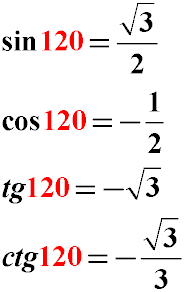
Синус, косинус і тангенс кута 2π / 3 радіан

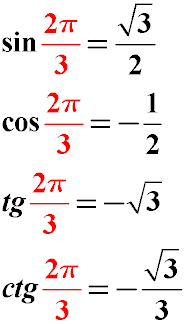
Нагадаємо собі, що 2π / 3 в градусах - це 120 градусів. (2 * 180/3 = 120). Таким чином, знайти значення тригонометричної функції для кута 2π / 3 і для Ула 120 градусів - це одне і те ж.

Як знайти значення тригонометричних функцій для кута 120 градусів

Знайдемо значення синуса, косинуса і тангенса для кута 120 градусів аналітичним способом.
На перший погляд, знаходження значень синуса, косинуса і тангенса для кута 120 градусів - завдання складне. Однак, це не зовсім так.
Перш за все, ми повинні звернути увагу, що для кутів, значення яких перевищує 90 градусів, у нас є формули приведення до кута, меншого 90 градусів..

Тому, для початку, уявімо собі кут в 120 градусів як (90 + 30)
тоді
sin ( 90 + α ) = cos α
sin 120 = sin( 90 + 30 ) = cos 30

cos ( 90 + α ) = - sin α
cos 120 = cos( 90 + 30 ) = -sin 30

tg ( 90 + α ) = -ctg α
tg 120 = tg( 90 + 30 ) = -ctg 30

Тепер можна подивитися значення в таблицях синуса, косинуса і тангенса 120 градусів, який перетворений в значення тригонометричних функцій синуса, косинуса і тангенса кута 30 градусів.
В уроці за посиланням можна подивитися як обчислити значення тригонометричних функцій для кута 30 градусів.

В результаті отримуємо:

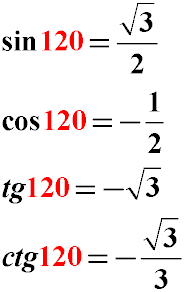
Як видно з прикладу, значення тригонометричних функцій кутів синуса, косинуса і тангенса 120 градусів можуть бути отримані шляхом нескладних тригонометричних перетворень з використанням тригонометричних тотожностей.

Див. також повну таблицю значень тригонометричних функцій (таблицю синусів, косинусів і тангенсів).

Нижче наведені також значення тригонометричних функцій для кута 120 градусів у вигляді десяткового дробу з чотирма знаками після коми.

2π/3	синус 120  sin 120	косинус 120 cos 120	тангенс 120 tg 120	котангенс 120 ctg 120
Значення	0,8660	-0,5000	-1,7321	-0,5774