|
|
Примітка. Це урок із розв'язками задач з геометрії (розділ циліндр). Якщо Вам необхідно вирішити задачу з геометрії,
якої тут немає – пишіть про це у форумі. У завданнях замість символу "квадратний корінь" можна використовувати знак "√".
Завдання
Осьовий переріз циліндра - квадрат, діагональ якого дорівнює 4√2.
Обчислити об'єм циліндра.
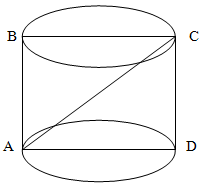
Рішення.
Оскільки діагональ перерізу циліндра – квадрат, то позначимо його сторону як a.
a2 + a2 = (4√2)2
2a2 = 32
a2 = 16
a = 4
Об'єм циліндра знайдемо за формулою:
V = πd2/4*h
звідки
V = π42/4*4
V = 16π
Відповідь: Об'єм циліндра дорівнює 16π
Завдання
Куб із ребром довжиною а вписаний у циліндр. Знайдіть площу осьового перерізу циліндра.
Рішення.
Проведемо площину через основу циліндра.

Квадрат вписаний у коло
Діагональ куба є одночасно діаметром циліндра. Знаючи бік куба, визначаємо довжину діагоналі AC квадрата ABCD як
CD2 + AD2 = AC2
a2 + a2 = AC2
2a2 = AC2
AC = a√2
Проведемо площину через вісь циліндра по діагоналі AC.
Висота перерізу дорівнює довжині ребра куба та за умовами задачі рана а, а ширина перерізу дорівнює a√2.
Таким чином, площа перерізу дорівнює:
S = a * a√2 = a2√2
Відповідь: a2√2
Завдання
Діагональ осьового перерізу циліндра дорівнює 12 см і утворює з площиною нижньої основи кут 45 градусів.
Знайти об'єм циліндра.
Рішення.
Оскільки основа осьового перерізу утворює з висотою циліндра, що належить перерізу, прямий кут, то трикутник,
утворений діагоналлю осьового перерізу, висотою циліндра та його діаметром - прямокутний.
Виходячи з цього, кут між діагоналлю і висотою також дорівнює 45 градусів (180 – 90 – 45).
Таким чином, трикутник є рівнобедреним, а отже, висота циліндра дорівнює його діаметру. Застосувавши теорему Піфагора, знайдемо їх.
d2 + d2 = 122
2d2 = 144
d2 = 72
Тепер застосуємо формулу об'єму циліндра V = пd2/4 h
V = 72п / 4 * √72
V = 18п * √72 = 18п * √(2 * 36) = 108п√2
Відповідь: 108п√2
Завдання
Висота циліндра 2м. Радіус основи 7м. У цей циліндр похило вписаний квадрат так, що всі вершини його лежать на околицях основ.
Знайти сторону квадрата.
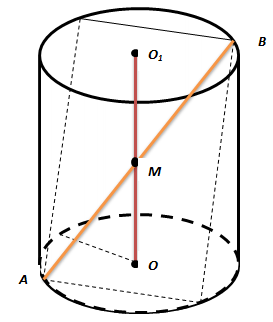
Рішення.
Циліндр із діагональним перетином
В силу симетричності квадрата і циліндра і через те, що квадрат похилий, діагональ квадрата перетне вісь циліндра ОО1 у точці М,
що є серединою відрізка ОО1. За умовою ОО1 = 2м, а ОА = 7 м, тому OМ = 1м.
Нехай d – діагональ квадрата. Тоді сторона квадрата а дорівнює:
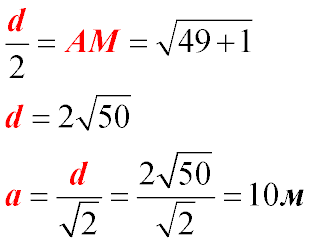
Осьовий переріз циліндра |
Описание курса
|

