Примітка. Див. також таблицю значень тригонометричних функцій для всіх кутів.

Синус 30, косинус 30, тангенс 30 градусів і синус 60, косинус 60, тангенс 60 градусів

Як були обчислені ці значення?
Також ви можете відразу перейти до: 

• табличні значення синуса, косинуса i тангенса 30 градусiв, 
• табличні значення синуса, косинуса и тангенса 60 градусiв.

На цій сторінці наведено покроковi пояснення логіки розрахунку даних значень, спочатку для кута тридцять градусів, а потім і шістдесят. Для цього проводиться побудова довільного прямокутного трикутника з відповідними кутами і обчислюється значення синуса, косинуса і тангенса 30 градусів, а в другій частині цієї статті - для кута 60 градусів.

Значення тригонометричних функцій синуса, косинуса, тангенса при α=30°

Розглянемо рiвнобiчний трикутник АВС. Хай, кожна з його сторін буде рівна а. Згідно з властивостями рівностороннього трикутника, всі його кути рівні, у тому числі кут ∠В=60°. 

Значення синуса, косинуса і тангенса ми можемо обчислити, якщо знайдемо співвідношення відповідних сторін для кута 30 градусів в прямокутному трикутнику. Оскільки значення цих тригонометричних функцій залежить виключно від градусної міри кута, то обчислені нами співвідношення і будуть значеннями синуса 30, косинуса 30 і тангенса 30 градусів. 

Спочатку зробимо додаткові побудови. З вершини А на сторону BC проведемо медіану АO.

Медіана АО у рівносторонньому трикутнику одночасно є бісектрисою і висотою.

Тоді тикутник АОВ - прямокутний з кутом ∠ВАО=30°. (Кут В дорівнює 60 градусам ∠ВOA прямій і дорівнює 90 градусам, отже ∠ВАО = 180 - 90 - 60 = 30 градусів)

Для отриманого прямокутного трикутника обчислимо значення тригонометричних функцій його кутів. Зробимо це спочатку для кута 30 градусів.

Величина гіпотенузи нам відома і рівна а. Катет OB рівний a/2, оскільки АO - медіана трикутника ABC. Знайдемо катет АТ.

По теоремі Піфагора:

АВ²=АО²+ОВ²;

АО²=АВ²-ОВ²

пiдставимо в одержане рiвняння значення гiпотенузи (намi прийнято, що воно равно а)

АО²=a²- (а/2)²

АО²=3a²/4  

AO=√( 3a²/4 ) =a√3/2

Тепер ми обчислили всі сторони прямокутного трикутника ABO. Враховуючи, що AB = a, OB = a/2, AO = a√3/2, iз спiввiдношень сторiн прямокутного трикутника розрахуємо одержанi значення. Згiдно визначенню сiнуса, косiнуса та тангенса:

sin 30 = OB / AB (за визначенням синуса - відношення катета, що протилежить, до гіпотенузи)

cos 30 = AO / AB (за визначенням косинуса - відношення прилеглого катета до гіпотенузи)

tg 30 = OB / AO (за визначенням тангенса - відношення катета, що протилежить, до прилеглого)

Звiдки маємо:

Враховуючи, що трикутник ABC - рiвнобiчний, то BO равно AB/2, а значення AO розраховано вище. В результатi одержуємо табличнi значення sin 30, cos 30 и tg 30 градусiв

Табличні значення sin 30, cos 30 і tg 30 градусів:

  

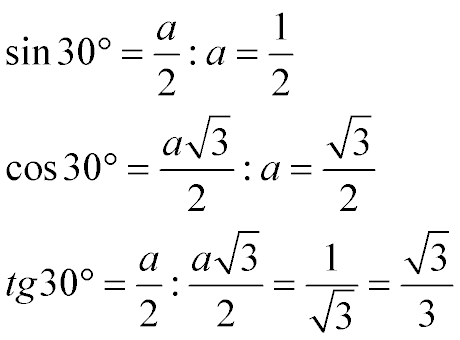
Тобто:
Тангенс 30 градусів дорівнює кореню з трьох на три
Синус 30 градусів дорівнює одній другій або 0,5
Косинус 30 градусів дорівнює кореню з трьох на два
Враховуючи таблицю формул приведення тригонометричних функцій,

Так як sin( 90°- 30°) = sin60°, а sin60°=cos30°, то:

Табличні значення sin 60, cos 60 і tg 60 градусів:

Як саме були обчислені ці функції, описано вище. Тут же наведені самі значення:

 

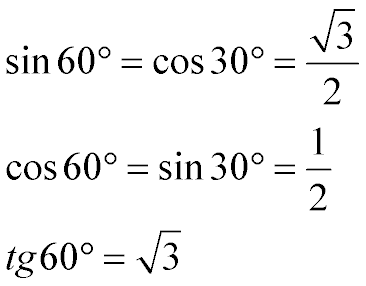
Тобто:   
Тангенс 60 градусів дорівнює кореню з трьох   
Синус 60 градусів дорівнює кореню з трьох на два   
Косинус 60 градусів рівний однією другою або 0,5 

Як видно з розрахунків, приведених вище, при обчисленні значення конкретної тригонометричної функції важливі не конкретні довжини сторін, а лише їх співвідношення, яке завжди буде однаковим для одних і тих же кутів, незалежно від розмірів трикутника. 

Синус, косинус и тангенс кута пі на 3 (π / 3)

У завданнях окрім градусної міри кута часто зустрічаються і позначення кута в радіанах. Міра радіану кута виражається через число пі, яке описує співвідношення довжини кола до її діаметру. Для простоти запам'ятовування правила переведення радіан в градуси i назад, пропоную завжди пам'ятати наступне: діаметр кола охоплює дугу величиною 180 градусів, що складає пі радіан. Оскільки всі величини кута в радіанах вказуються через число пі, то для переведення в градусну міру досить замінити число пі на 180 градусів. 

Тому, візьмемо до уваги, що кут пі на 3 дорівнює 60 градусам. (180 / 3 = 60) 

Звідки: 

• Тангенс π/3 (пі на три) радіан дорівнює кореню з трьох   
• Синус π/3 (пі на три) радіан дорівнює кореню з трьох на два   
• Косинус π/3 (пі на три) радіан рівний однієї другої (1/2) або 0,5

Щоб ці значення було зручно запам'ятати візуально, вони наведені на малюнку нижче.

Синус, косинус і тангенс кута пі на 6 (π/6)

Виходячи з написаного вище принципу переведення радіан в градуси, кут пі на 6 дорівнюватиме 
180 / 6 = 30 градусів.  

Звідки: 

• Тангенс пі на 6 (π/6) дорівнює кореню з трьох на три 
• Синус пі на 6 (π/6) дорівнює однієї другої (1/2) або 0,5 
• Косинус пі на 6 (π/6) дорівнює кореню з трьох на два 

Для зручнішого візуального сприйняття ці значення приведені нижче на малюнку

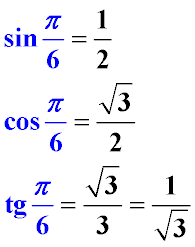
Примітка. Дана стаття показує, як обчислюється значення sin 60, cos 60 і подібних значень. Якщо Ви хочете подивитися зведену довідкову інформацію - перейдіть на таблицю значень тригонометричних функцій