|
|
Примітка. Для отримання довідкової інформації див також формули перетворення тригонометричних функцій.
Загальний принцип перетворення функцій виду α + a/bπ до більш простого вигляду
Щоб здійснити приведення кута тригонометричної функції, необхідно надати аргумент функції у вигляді:
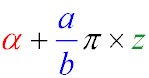
Після цього можна буде скористатися правилами та формулами, які вказані нижче.
Правило 1. Якщо a = 2, а z - натуральне число, то назва функції не змінюється
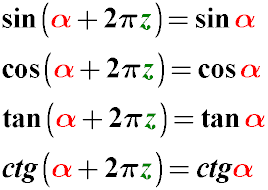
Синус альфа плюс два пі дорівнюватиме синус альфа.
Косинус альфа плюс два пі дорівнюватиме косинус альфа.
Тангенс альфа плюс два пі дорівнюватиме тангенс альфа.
Котангенс альфа плюс два пі дорівнюватиме котангенс альфа.
Дані рівності випливають із властивостей тригонометричного кола.
Приклад. Приведемо до простішого вигляду вираз cos 390.
Візьмемо до уваги, що π = 180 градусів, тоді
cos 390 = cos (30 + 2π)
Тепер скористаємося формулою (2) приведення на малюнку вище
cos (30 + 2π) = cos 30
Правило 2. Віднімання з 2π кута α
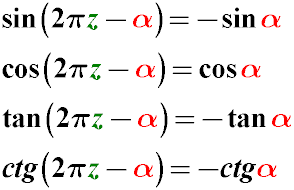
Синус два пі мінус альфа дорівнюватиме мінус синус альфа.
Косинус два пі мінус альфа дорівнює косинус альфа.
Тангенс два пі мінус альфа дорівнює мінус тангенс альфа.
Котангенс два пі мінус альфа дорівнює мінус котангенс альфа.
Дані властивості випливають із властивостей тригонометричного кола з урахуванням парності функцій.
Приклад. Приведемо до більш простого вигляду вираз sin 345.
Візьмемо до уваги, що π = 180 градусів, тоді
sin 345 = sin ( 2π - 15 )
Тепер скористаємося формулою (1) приведення на малюнку вище, тоді
sin ( 2π - 15 ) = - sin 15
Правило 3. Додавання кута з π/2
Якщо аргумент тригонометричної функції містить вираз π/2 або n*π/2, де n – натуральне непарне число, то функція
змінюється за такими правилами:
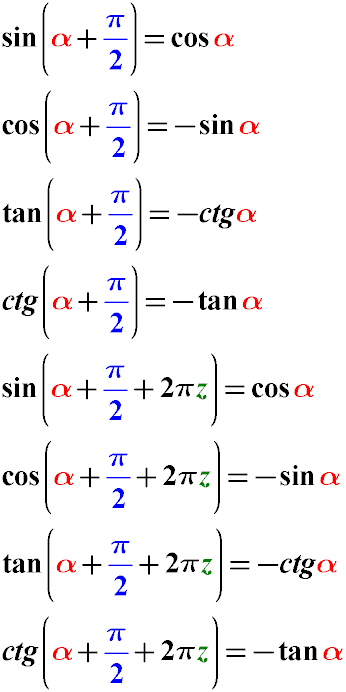
Синус кута альфа плюс пі на два дорівнює косінус того ж кута.
Косинус альфа плюс пі на два дорівнює мінус косинус альфа.
Тангенс альфа плюс пі на два дорівнює мінус котангенс альфа.
Котангенс альфа плюс пі на два дорівнює мінус тангенс альфа.
З властивостей тригонометричного кола випливає, що:
Синус кута альфа плюс пі на два плюс два пі дорівнює косінусу того ж кута.
Косинус альфа плюс пі на два плюс два пі дорівнює мінус косинус альфа.
Тангенс альфа плюс пі на два плюс два пі дорівнює мінус котангенс альфа.
Котангенс альфа плюс пі на два плюс два пі дорівнює мінус тангенс альфа.
Приклад. Приведемо до простішого вигляду вираз sin ( α + 5π/2 ).
sin ( α + 5π/2 ) = sin (α + π/2 + 2π*1)
sin (α + π/2 + 2π*1) = cos α
Правило 4. Формули віднімання кута з π/2 (π/2 - α)
Якщо в аргументі тригонометричної функції є віднімання кута значення π/2, наприклад cos( π/2 - α ),
тоді можна скористатися такими формулами перетворення аргументу:
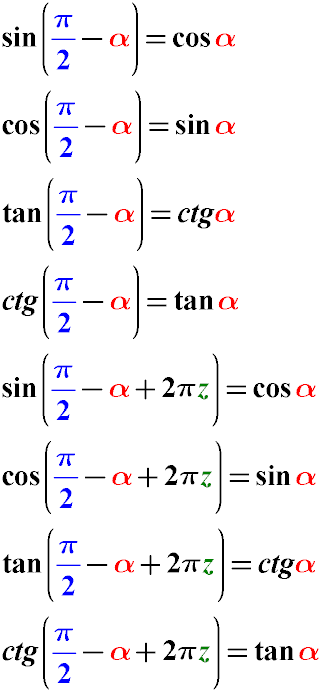
З властивостей прямокутного трикутника випливає, що:
Синус кута на два мінус альфа дорівнює косинусу альфа.
Синус кута на два мінус альфа дорівнює синусу альфа.
Тангенс пі на два мінус альфа дорівнює конангенсу альфа.
Котангенс кута на два мінус альфа дорівнює тангенсу альфа.
З властивостей тригонометричного кола випливає, що:
Синус кута пи на два мінус альфа плюс два пирі дорівнює косинусу альфа.
Синус кута пи на два мінус альфа плюс два пи дорівнює синусу альфа.
Тангенс пі на два мінус альфа плюс два пи дорівнює конангенсу альфа.
Котангенс кута на два мінус альфа плюс два пирі дорівнює тангенсу альфа.
Приклад. Приведемо до більш простого вигляду вираз cos (5π/2 - α).
cos ( 5π/2 - α ) = cos( π/2 - α + 2π * 1)
cos( π/2 - α + 2π * 1) = sin α
Правило 5. Тригонометричні формули приведення кута α + π
Якщо аргумент тригонометричної функції можна подати як суму кутів виду α + π + 2πz, то така функція може бути
наведена до більш простого вигляду за допомогою таких формул:
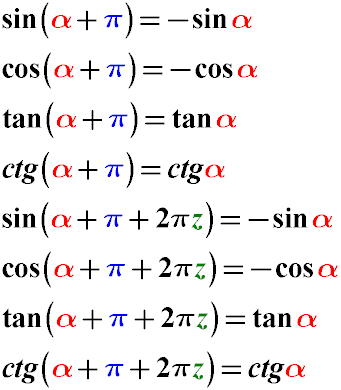
Синус альфа плюс пи дорівнює мінус синус альфа.
Косинус альфа плюс пи дорівнює мінус косинус альфа.
Тангенс альфа плюс пи дорівнює тангенс альфа.
Контангенс альфа плюс пи дорівнює котангенс альфа.
також
Синус альфа плюс пі плюс два пі дорівнює мінус синус альфа.
Косинус альфа плюс пі плюс два пі дорівнює мінус косинус альфа.
Приклад. Приведемо до більш простого вигляду вираз sin (7π + α)
sin (7π + α) = sin (π + α + 2π * 3)
sin (π + α + 2π * 3) = - sin α
Правило 6. Тригонометричні формули приведення для кута ( π - α )
Якщо в аргументі тригонометричної функції потрібно відняти кут з π, тобто спростити аргумент функції виду (π - α),
можна скористатися такими формулами:
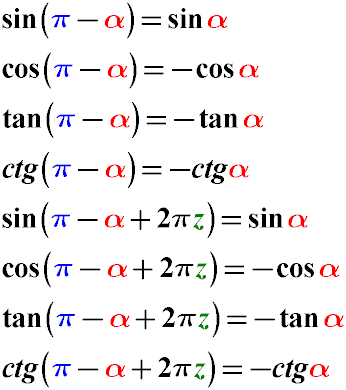
Приклад. Приведемо до більш простого вигляду вираз sin (5π - α).
sin ( 5π -α ) = sin ( π - α + 2π * 2 )
sin (π - α + 2π * 2) = sin α
Правило 7. Тригонометричні формули приведення функцій для кутів ( 3π / 2 + α )
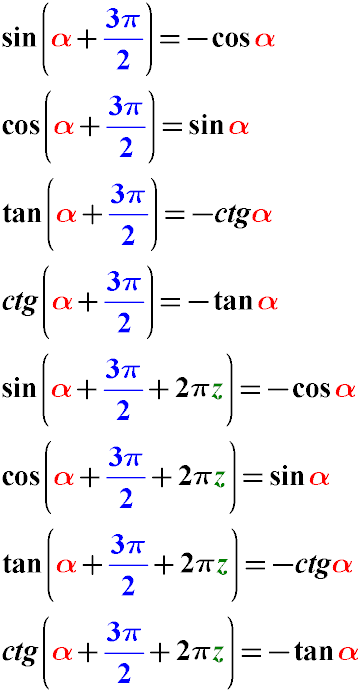
Приклад. Приведемо вираз cos (α + 7π/2) до більш простого вигляду.
cos(α+7π/2) = cos(α+3π/2+2π*1)
cos (α + 3π/2 + 2π * 1) = sin α
Правило 8. Тригонометричні формули наведення аргументу для випадків віднімання кута α з 3 π / 2
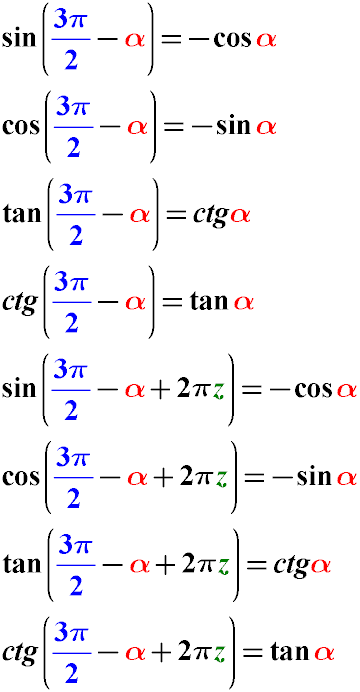
Приклад. Приведемо вираз sin (7π/2 - α) до більш простого вигляду.
sin ( 7π/2 - α ) = sin( 3π/2 - α + 2π * 1)
sin( 3π/2 - α + 2π * 1) = - cos α
Доказ правильності формул перетворення тригонометричних функцій виду (α + a/bπ)
ЗНАЧЕННЯ СИНУСУ, КОСИНУСУ І ТАНГЕНСУ гострих кутів
Значення тригонометричних функцій гострих кутів виводяться із співвідношення сторін прямокутного трикутника.
ТЕОРЕМА: Для будь-якого гострого кута α:
sin (90°- α)=cos α;
cos (90°- α)=sin α;
tg (90 ° - α) = ctg α.
Розглянемо прямокутний трикутник із гострим кутом α. За теоремою Піфагора:
АС2 = АВ2 + ВС2.
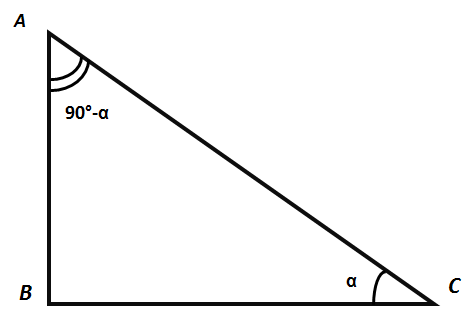
За визначенням тригонометричних функцій:
sin α= АВ/АС та cos α= ВС/АС (1)
Оскільки ∠А + ∠С = 90°, то
∠А = 90°- ∠С
∠ А=90°-α,
sin (90°-α)=ВС/АС та cos (90°-α)=АВ/АС (2)
Порівняємо рівності (1) і (2) і запишемо тотожні рівністі:
sin (90 ° - α) = cos α; cos (90 ° - α) = sin α (3)
Обчислимо tg (90°- α), знаючи, що тангенс кута дорівнює відношенню синуса і косинуса того ж кута і використовуючи рівність (3):
tg (90 ° - α) = sin (90 ° - α) / cos (90 ° - α) = cos α / sin α = ctg α.
Косинус подвійного кута |
Описание курса
| Тригонометричні формули зниження ступеня sin cos tan
|

