|
|
Діагоналі трапеції
Властивості діагоналей трапеції
- Відрізок, що з'єднує середини діагоналей трапеції, дорівнює половині різниці основ
- Трикутники, утворені основами трапеції та відрізками діагоналей до точки їх перетину - подібні
- Трикутники, утворені відрізками діагоналей трапеції, сторони яких лежать на бічних сторонах трапеції – рівновеликі (мають однакову площу)
- Якщо продовжити бічні сторони трапеції у бік меншої основи, то вони перетнуться в одній точці з прямої, що з'єднує середини основ
- Відрізок, що з'єднує основи трапеції, і проходить через точку перетину діагоналей трапеції, ділиться цією точкою в пропорції, що дорівнює співвідношенню довжин основ трапеції
- Відрізок, паралельний основам трапеції, і проведений через точку перетину діагоналей, ділиться цією точкою навпіл, а його довжина дорівнює 2ab/(a + b), де a і b - основи трапеції
Властивості відрізка, що з'єднує середини діагоналей трапеції
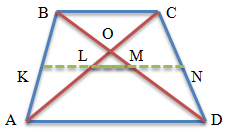
З'єднаємо середини діагоналей трапеції ABCD, у результаті з'явиться відрізок LM.
Відрізок, що з'єднує середини діагоналей трапеції, лежить на середній лінії трапеції.
Даний відрізок паралельний основам трапеції.
Довжина відрізка, що з'єднує середини діагоналей трапеції, дорівнює напіврізниці її основ.
LM = (AD - BC)/2
або
LM = (a-b)/2
Властивості трикутників, утворених діагоналями трапеції
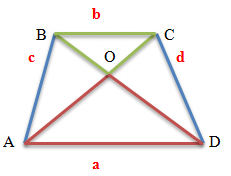
Трикутники, які утворені основами трапеції та точкою перетину діагоналей трапеції – є подібними.
Трикутники BOC та AOD є подібними. Оскільки кути BOC та AOD є вертикальними – вони рівні.
Кути OCB і OAD є внутрішніми навхрест лежачими при паралельних прямих AD і BC (підстави трапеції паралельні між собою) і прямій AC, отже, вони рівні.
Кути OBC і ODA рівні з тієї ж причини (внутрішні навхрест лежачі).
Оскільки всі три кути одного трикутника дорівнюють відповідним кутам іншого трикутника, то ці трикутники подібні.
Що з цього випливає?
Для вирішення задач з геометрії подібність трикутників використовується так.
Якщо нам відомі значення довжин двох відповідних елементів подібних трикутників, то знаходимо коефіцієнт подібності (ділимо одне на інше).
Звідки довжини всіх інших елементів співвідносяться між собою таким самим значенням.
Властивості трикутників, що лежать на бічній стороні та діагоналях трапеції
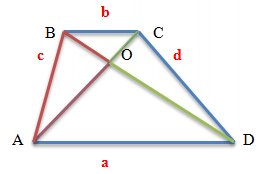
Розглянемо два трикутники, що лежать на бічних сторонах трапеції AB та CD.
Це – трикутники AOB та COD. Незважаючи на те, що розміри окремих сторін у цих трикутників можуть бути різними,
але площі трикутників, утворених бічними сторонами і точкою перетину діагоналей трапеції рівні, тобто трикутники є рівновеликими.
Властивості трапеції, добудованої до трикутника
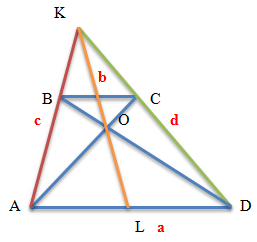
Якщо продовжити сторони трапеції у бік меншої основи, то точка перетину сторін співпадатиме з прямою лінією, яка проходить через середини основ.
Таким чином, будь-яка трапеція може бути добудована до трикутника. При цьому:
- Трикутники, утворені основами трапеції із загальною вершиною в точці перетину продовжених бічних сторін, є подібними.
-
Пряма, що з'єднує середини основ трапеції, є одночасно медіаною побудованого трикутника
Властивості відрізка, що з'єднує основи трапеції
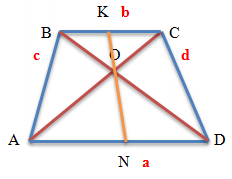
Якщо провести відрізок, кінці якого лежать на підставах трапеції, який лежить на точці перетину діагоналей трапеції (KN),
то співвідношення складових його відрізків від сторони основи до точки перетину діагоналей ( KO/ON )
буде дорівнює співвідношенню основ трапеції ( BC/AD ).
KO / ON = BC / AD
Ця властивість випливає з відповідності відповідних трикутників (див. вище).
Властивості відрізка, паралельного основам трапеції
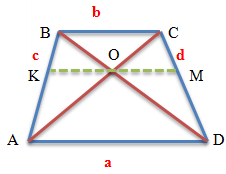
Якщо провести відрізок, паралельний основам трапеції і проходить через точку перетину діагоналей трапеції,
то він матиме наступні властивості:
- Заданий відрізок (KM) ділиться точкою перетину діагоналей трапеції навпіл
-
Довжина відрізка, що проходить через точку перетину діагоналей трапеції та паралельного основам, дорівнює KM = 2ab/(a + b)
Формули для знаходження діагоналей трапеції
Далі наведено формули, що відображають залежність між сторонами, кутами трапеції та величиною її діагоналей.
Ці формули стануть у нагоді для вирішення задач з геометрії на тему "діагоналі трапеції"
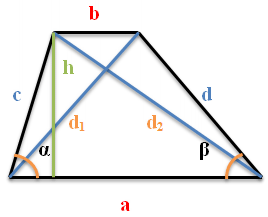
Далі, у формулах використовуються такі позначення:
a, b - основи трапеції
c, d - бічні сторони трапеції
d1 d2 - діагоналі трапеції
α β - кути при більшій основі трапеції
Формули знаходження діагоналей трапеції через основи, бічні сторони та кути при основі

Перша група формул (1-3) відображає одну з основних властивостей діагоналей трапеції:
1. Сума квадратів діагоналей трапеції дорівнює сумі квадратів бічних сторін плюс подвоєний добуток її основ. Ця властивість діагоналей трапеції може бути доведена як окрема теорема
2. Ця формула отримана шляхом перетворення попередньої формули. Квадрат другої діагоналі перекинутий через знак рівності, після чого з лівої та правої частини виразу витягнуто квадратний корінь.
3. Ця формула знаходження довжини діагоналі трапеції аналогічна попередньої, з тією різницею, що в лівій частині виразу залишена інша діагональ
Наступна група формул (4-5) аналогічна за змістом та виражає аналогічне співвідношення.
Група формул (6-7) дозволяє знайти діагональ трапеції, якщо відома більша основа трапеції, одна бічна сторона та кут при основі.
Формули знаходження діагоналей трапеції через висоту
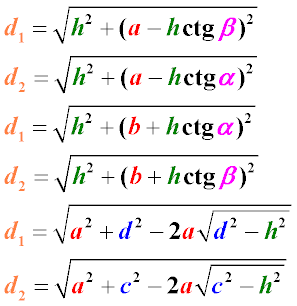
Примітка. У цьому уроці наведено розв'язання задач з геометрії про трапеції.
Якщо Ви не знайшли рішення задачі з геометрії, що Вас цікавить типу - задайте питання на форумі.
Завдання.
Діагоналі трапеції ABCD (AD | | ВС) перетинаються в точці О.
Знайдіть довжину основи ВС трапеції, якщо основа АD = 24 см, довжина АВ = 9см, довжина ОС = 6 см.
Рішення.
Розв'язання цього завдання з ідеології є абсолютно ідентичним попереднім завданням.
Трикутники AOD і BOC є подібними за трьома кутами - AOD і BOC є вертикальними, а інші кути попарно рівні,
оскільки утворені перетином однієї прямої і двох паралельних прямих.
Оскільки трикутники подібні, всі їх геометричні розміри ставляться між собою,
як геометричні розміри відомих нам за умовою завдання відрізків AO і OC.
Тобто
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Відповідь: 16 см
Завдання.
У трапеції ABCD відомо, що AD=24, ВС=8, АС=13, BD=5√17.
Знайдіть площу трапеції.
Рішення.
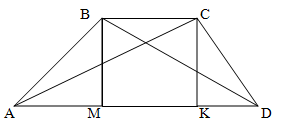
Для знаходження висоти трапеції з вершин меншої основи B і C опустимо на більшу основу дві висоти.
Оскільки трапеція нерівнобока - позначимо довжину AM = a, довжину KD = b
(не плутати з позначеннями у формулі знаходження площі трапеції).
Оскільки основи трапеції паралельні, а ми опускали дві висоти, перпендикулярні більшій основі, то MBCK - прямокутник.
Значить
AD = AM+BC+KD
a + 8 + b = 24
a = 16 - b
Трикутники DBM і ACK - прямокутні, тому їх прямі кути утворені висотами трапеції.
Позначимо висоту трапеції через h. Тоді за теоремою Піфагора
h2 + (24 - a)2 = (5√17)2
и
h2 + (24 - b)2 = 132
Врахуємо, що a = 16 - b тоді в першому рівнянні
h2 + (24 - 16 + b)2 = 425
h2 = 425 - (8 + b)2
Підставимо значення квадрата висоти у друге рівняння, отримане за Теоремою Піфагора.
Отримаємо:
425 - (8 + b)2 + (24 - b)2 = 169
-(64 + 16b + b)2 + (24 - b)2 = -256
-64 - 16b - b2 + 576 - 48b + b2 = -256
-64b = -768
b = 12
Таким чином, KD = 12
Звідки
h2 = 425 - (8 + b)2 = 425 - (8 + 12)2 = 25
h = 5
Знайдемо площу трапеції через її висоту та напівсуму основ
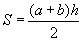 , де a b - основи трапеції, h - висота трапеції , де a b - основи трапеції, h - висота трапеції
S = (24 + 8) * 5 / 2 = 80 см2
Відповідь: площа трапеції дорівнює 80 см2.
Прямокутна трапеція |
Описание курса
| Паралелограм
|

