|
Примітка. В даному уроці викладені теоретичні матеріали і рішення задач з геометрії на тему "медіана в прямокутному трикутнику". Якщо Вам необхідно вирішити задачу з геометрії, якої тут немає - пишіть про це в форумі. Майже напевно, курс буде доповнений.
Властивості медіани прямокутного трикутника
Визначення медіани
Медіана трикутника - це відрізок, що з'єднує один з кутів трикутника з серединою протилежної йому сторони. (Медіаною також називають пряму, що містить даний відрізок)
|
-
Медіани трикутника перетинаються в одній точці і діляться цією точкою на дві частини у відношенні 2:1, рахуючи від вершини кута. Точка їх перетину називається центром ваги трикутника (відносно рідко в задачах для позначення цієї точки використовується термін "центр ваги");
-
Медіана розбиває трикутник на два рівновеликих трикутника;
- Трикутник ділиться трьома медіанами на шість рівновеликих трикутникiв;
- Більшій стороні трикутника відповідає менша медіана.
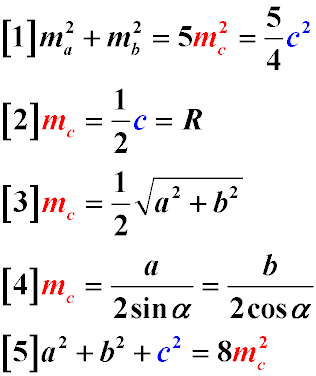
Задачі по геометрії, запропоновані для вирішення, в основному, використовують такі властивості медіани прямокутного трикутника:.
-
Сума квадратів медіан, що проведені до катетів прямокутного трикутника, дорівнює п'яти квадратам медіан, що проведені до гіпотенузи (Формула 1);
- Медіана, що проведена до гіпотенузи прямокутного трикутника, дорівнює половині гіпотенузи (Формула 2);
- Медіана, що проведена до гіпотенузи прямокутного трикутника, дорівнює радіусу кола, описаного навколо даного прямокутного трикутника (Формула 2);
- Медіана, що проведена до гіпотенузи, дорівнює половині квадратного кореня з суми квадратів катетів (Формула 3);
- Медіана, що проведена до гіпотенузи, дорівнює частці від ділення довжини катета на два синуси протилежного до катету гострого кута (Формула 4);
- Медіана, що проведена до гіпотенузи, дорівнює частці від ділення довжини катета на два косинуси прилеглого до катету гострого кута (Формула 4);
- Сума квадратів сторін прямокутного трикутника дорівнює восьми квадратам медіани, що проведена на його гіпотенузу (формула 5).
Позначення в формулах:
a, b - катети прямокутного трикутника;
c - гіпотенуза прямокутного трикутника;
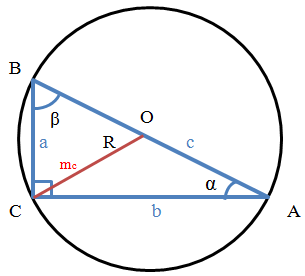
Якщо позначити трикутник, як ABC, то
ВС = а
AC = b
AB = c
(Тобто сторони a, b, c - є протилежними відповідним кутам)
ma - медіана, проведена до катету а
mb - медиана, проведенная к катету b
mc - медіана прямокутного трикутника, проведена до гіпотенузи c
α (альфа) - кут CAB, протилежний стороні а
Задача про медиану в прямоугольном треугольнике
Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно, 3 см и 4 см. Найдите гипотенузу треугольника
Решение
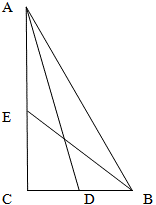
Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике. В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y).
Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC - общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора
AC2 + CD2 = AD2
Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4x2 + y2 = 9
Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
По теореме Пифагора:
EC2 + BC2 = BE2
Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x2 + 4y2 = 16
Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений.
4x2 + y2 = 9
x2 + 4y2 = 16
Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5x2 + 5y2 = 25
5( x2 + y2 ) = 25
x2 + y2 = 5
Обратимся к исходному треугольнику ABC. По теореме Пифагора
AC2 + BC2 = AB2
Так как длина каждого из катетов нам "известна", мы приняли, что их длина равна 2x и 2y, то есть
4x2 + 4y2 = AB2
Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки
4 ( x2 + y2 ) = AB2
Чему равно x2 + y2 мы уже знаем (см. выше x2 + y2 = 5), поэтому просто подставим значения вместо x2 + y2
AB2 = 4 х 5
AB2 = 20
AB = √20 = 2√5
Ответ: длина гипотенузы равна 2√5
Гіпотенуза прямокутного трикутника |
Описание курса
| Чотирикутник
|

