Властивості довжин сторін чотирикутника

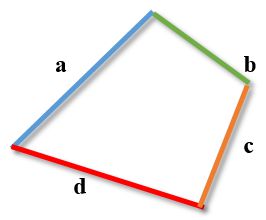
Модуль різниці будь-яких двох сторін чотирикутника не перевищує суми двох інших його сторін.

|a -b| ≤ c + d
|a -c| ≤ b + d
|a -d| ≤ b + c
|b -c| ≤ a + d
|b -d| ≤ a + b
|c -d| ≤ a + b

Важливо. Нерівність є вірною для будь-якої комбінації сторін чотирикутника. Малюнок наведено виключно для полегшення сприйняття.

У будь-якому чотирикутнику сума довжин трьох його сторін не менше довжини четвертої сторони.

a ≤ b + c + d
b ≤ a + c + d
c ≤ a + b + d
d ≤ a + b + c

Важливо. При вирішенні завдань в межах шкільної програми можна використовувати суворе нерівність (<). Рівність досягається тільки в разі,
якщо чотирикутник є "виродженим", тобто три його точки лежать на одній прямій. Тобто ця ситуація не підпадає під класичне визначення
чотирикутника.

Завдання про можливість існування чотирикутника із заданими сторонами

Завдання 1

Чи існує чотирикутник, якщо довжини сторін 1 см, 3 см, 5 см, 9 см?

Рішення:

Для того, щоб чотирикутник існував, необхідно, щоб довжина будь-якої з його сторін була меншою, ніж сума довжин трьох інших сторін.
Інакше буде неможливо замкнути периметр.

Для перевірки візьмемо найбільшу із сторін (9 см). Тоді сума решти становитиме:

Це означає, що довжини цих сторін або повинні бути відкладені як частина відрізка (9 см) більшої сторони, або таку фігуру замкнути неможливо.
Висновок: такий чотирикутник не може існувати.

Відповідь: Ні, не існує.

Завдання 2

Чи існує чотирикутник, якщо довжини сторін 5 см, 17 см, 3 см, 7 см?

Рішення:

Для того, щоб чотирикутник існував, необхідно, щоб довжина будь-якої з його сторін була меншою, ніж сума довжин трьох інших сторін.
Інакше буде неможливо замкнути периметр.

Для перевірки візьмемо найбільшу із сторін (17 см). Тоді сума решти становитиме:

Це означає, що таку фігуру замкнути неможливо. Висновок: такий чотирикутник не може існувати.

Відповідь: Ні, не існує.