|
|
Паралелограм - чотирикутник, у якого протилежні сторони попарно паралельні, тобто лежать на паралельних прямих.
Приватними випадками паралелограм є прямокутник, квадрат і ромб.
Як виглядає паралелограм
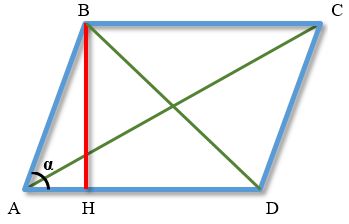
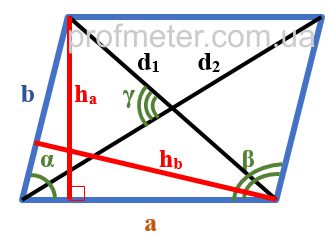
На наведеному малюнку паралелограм позначений синіми лініями.
Елементи паралелограма, вказані на малюнку:
ABCD - паралелограм, у якого протилежні сторони попарно паралельні (AB паралельна CD, а BC паралельна AD)
BH – висота паралелограма, опущена з точки B на основу AD (на малюнку позначена червоним кольором)
AC та BD - діагоналі паралелограма.
Властивості паралелограма
- Протилежні сторони паралелограма рівні
-
Протилежні кути паралелограма рівні
-
Діагоналі паралелограма перетинаються і точкою перетину діляться навпіл. Точка перетину діагоналей називається центром симетрії паралелограма
-
Діагональ ділить паралелограм на два рівні трикутники
-
Сума кутів, що прилягають до одного боку, дорівнює 180 °. (Див. формулу нижче)
-
Сума всіх кутів дорівнює 360 °
-
Середні лінії паралелограма перетинаються в точці перетину його діагоналей і діляться цією точкою навпіл
-
Сума квадратів діагоналей паралелограма дорівнює подвоєній сумі квадратів його сторін (див. формулу нижче)
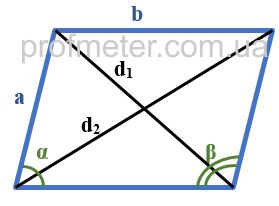
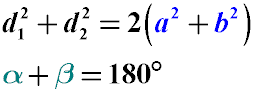
Ознаки паралелограма
Чотирикутник ABCD є паралелограмом, якщо виконується одна з наступних умов:
- Протилежні сторони попарно рівні
-
Протилежні сторони попарно паралельні та рівні
-
Протилежні кути попарно рівні
-
Діагоналі діляться в точці їхнього перетину навпіл
-
Сума сусідніх кутів дорівнює 180 градусів
-
Дві сторони рівні та паралельні
Як знайти площу паралелограма
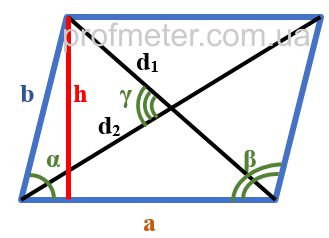
Формули знаходження площі паралелограма наведені нижче:
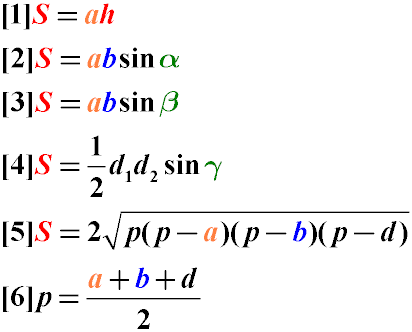
Тобто:
- Площа паралелограма дорівнює добутку довжини однієї з його сторін на висоту, опущену на цей бік
-
Площа паралелограма дорівнює добутку двох його суміжних сторін на синус кута між ними. Як видно з креслення, добуток b sin α дорівнює висоті, опущеній на інший бік, що в результаті дає нам попередню формулу
-
Площа паралелограма дорівнює добутку двох його суміжних сторін на синус кута між ними
-
Площа паралелограма дорівнює половині твору його діагоналей на синус кута між ними
-
Площу паралелограма також можна знайти через формулу Герона, розглянувши одну з діагоналей як трикутник і обчисливши подвоєну площу цього трикутника
-
Для знаходження напівпериметра трикутника з попередньої формули ми використовуємо дві сторони паралелограма та його діагональ. Оскільки кожна діагональ розбиває його на два рівні трикутники, то не має значення, яку з діагоналей ми виберемо
Як знайти сторони паралелограма
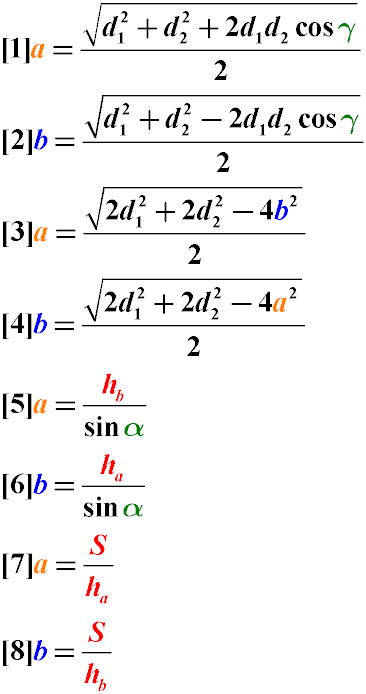
Сторони паралелограма можна знайти через:
- Розміри діагоналей та кут між ними (формули 1 та 2)
-
Через довжини діагоналей та одну зі сторін можна знайти другу (формули 3 та 4)
-
Через висоту, опущену на бік та кут між сторонами (формули 5 та 6)
-
Через площу та висоту, опущену на задану сторону, можна знайти величину цієї сторони (Формули 7 та 8)
Як знайти діагоналі паралелограма

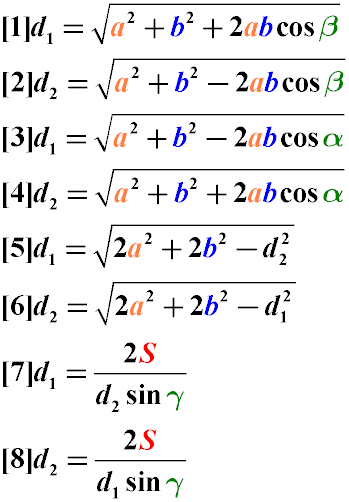
- Діагональ паралелограма можна знайти через довжини його сторін та косинус кута між ними (Формули 1-4)
- Також діагональ може бути знайдена через довжини сторін та розмір другої діагоналі (Формули 5-6)
- Діагональ може бути знайдена з площі, довжини другої діагоналями та кута між ними (Формули 7-8)
Як знайти периметр паралелограма

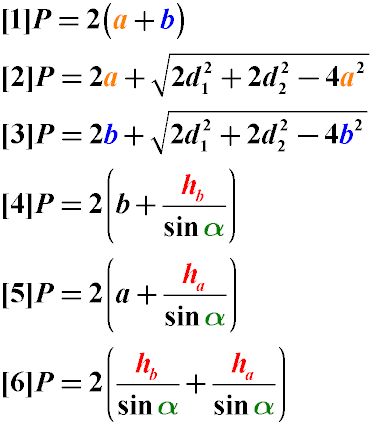
Периметр паралелограма можна знайти:
через його сторони (Формула 1)
через одну зі сторін та довжину двох діагоналей (Формули 2 та 3)
через бік, висоту та кут між сторонами (Формули 4-6)
Завдання з рішеннями про паралелограм дивіться на уроках нижче
Діагоналі трапеції |
Описание курса
| Висота паралелограма
|

