АКСІОМА 1. ВЛАСТИВОСТІ НАЛЕЖНОСТІ ТОЧОК І ПРЯМИХ НА ПЛОЩИНІ

Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, і тільки одну.

Дане твердження є аксіомою, тобто воно спочатку приймається як вірне і доказу не підлягає.

Коментарi

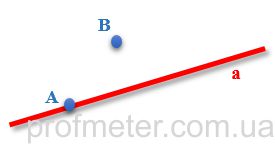
На малюнку нижче, позначені точки A і B. При цьому точка A належить прямій a, а точка B - не належить.Точки позначені синім кольором, пряма - червоним.

Примітка. Точки на малюнках зазвичай позначаються великими буквами, а прямі - малими.

Якщо точка належить прямій (Мал.1), то короткий запис такий: А ∈ а (читається як: «точка А належить прямій«а»). Якщо точка не належить прямій, то короткий запис такий: В ∉ а (читається як: «точка В не належить прямій а»).

 

Якщо взяти дві неспівпадаючі точки (А і С), то через них можна провести тільки одну пряму (а), хоча через кожну з цих точок можна провести безліч прямих (Мал.2)

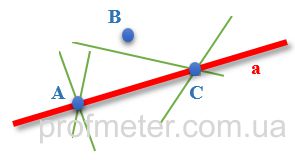
Примітка. Коли прямий належать дві точки (в даному випадку A і C), то вона може бути також описана як пряма AC, при цьому потрібно розуміти, що позначення a (мала буква a) і AC відноситься до однієї і тієї ж прямої.
Пояснення. Оскільки через дві точки (див. Аксіому) можна провести тільки одну пряму, то позначень цієї прямої може бути кілька, а сенс залишається тим же самим.

Якщо точки А і С збігаються (на кресленні в цьому випадку одна точка буде позначена двома літерами), то через них можна провести безліч прямих.

Описана вище аксіома є базовою для Евклідовій геометрії. На підставі даної аксіоми будуються докази багатьох теорем.