Два промені, що виходять з однієї точки, обмежують собою частину площини, яка розташована між променям. Фігура, яка при цьому утворюється, називається кутом. Промені із загальною вершиною в точці початку променів, називаються сторонами кута. Вершина кута розташована в точці початку променів.

Кут - частина площини, обмежена двома променями, що виходять з однієї точки.

Кут - це геометрична фігура, що має вершину, сторони і свою градусну міру.

Площина ділиться сторонами кута на дві частини. Менший з кутів називають внутрішнім, більший - зовнішнім. Для того, щоб не було різних тлумачень, про який з кутів йдеться, його сторони на кресленні з'єднують дугою. (Див. Рисунок)

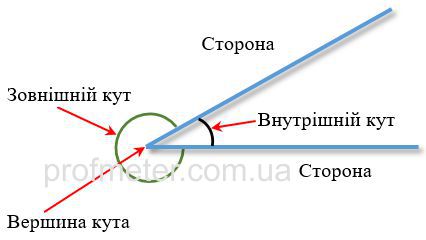
Кутова міра кута

• рівним кутах відповідає рівна кутова міра

• меншому куту відповідає менша кутова міра;

• у кута, сторони якого збігаються (нульового кута), кутова міра дорівнює нулю (то ж справедливо і для кута між паралельними прямими);

• кожен ненульовий кут має певну кутову міру, більшу від нуля;

• (Адитивність) кутова міра кута дорівнює сумі кутових мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.

Кут вимірюють в градусах, радіанах, градах і оборотах.

1 оборот = 360 градусів = 2π радіан = 400 град

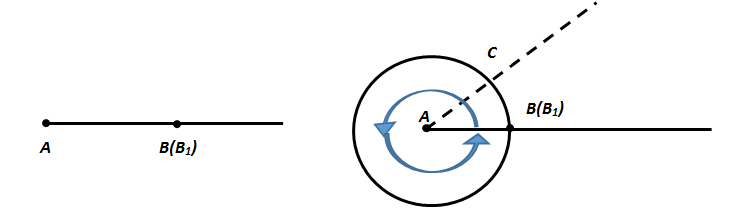
Розглянемо кут (на малюнку нижче), сторони якого збігаються (∠ВАВ₁). Його градусна міра дорівнює 0°

Якщо одну сторону кута (АВ) закріпити а другу сторону (АВ₁) обертати проти годинникової стрілки до тих пір, поки вона не співпаде з першою стороною (АВ), то площина такого кута складе повний кут (див. мал.). 

Отже, кут А (позначається ∠А) - це повний кут.

Позначення кутів

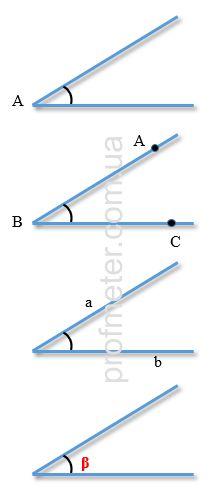
Кут може бути позначений як комбінація знака кута і його вершини, наприклад ∠А (мал.1);   

Також кут може позначатися за допомогою латинських великих літер (мал.2). Наприклад ∠ABC - це кут з вершиною B, сторони якого - це промені BA і BC.

Може зустрічатися позначення як значок кута із зазначенням сторін кута (наприклад ∠ аb). (мал.3)

Кут може позначатися грецькими буквами α, β, γ і так далі (мал.4). Виняток становить тільки буква "π". Її для позначення кутів не використовують.

Градусна міра кута

Якщо взяти повний кут і розділити його на 360 частин (кутів), то кожна частина, складова 1/360 частина повного кута, називається кутовим радіусом (позначається 1 °).

Отже, повний кут дорівнює 360 °.

Половина повного кута складе розгорнутий кут, який дорівнює 360 ° / 2 = 180 °.

Центральний і вписаний в коло кут

• Вписані кути, що спираються на одну й ту ж дугу окружності - рівні.
• Величина вписаного кута, що спирається на ту ж саму дугу окружності, що і центральний кут, дорівнює половині величини такого центрального кута.