АКСІОМА 8

ІСНУВАННЯ ТРИКУТНИКА, РІВНОГО ДАНОМУ

Яким би не був трикутник, існує рівний йому трикутник у заданому розташуванні щодо даної напівпрямої.

Задавши будь-який напрямок прямої, на ній можна завжди побудувати трикутник, що дорівнює даному.

Два трикутники можуть відрізнятися один від одного по довжині сторін, градусній мірі кутів, але їх розташування на площині (орієнтація)
не впливає на рівність чи нерівність трикутників.

Трикутники називаються рівними, якщо у них відповідні сторони та кути рівні.

Додаткові відомості

1. Копіювання трикутника: Для побудови трикутника, що дорівнює даному, можна використовувати метод копіювання. Це включає вимір всіх
   сторін і кутів вихідного трикутника та побудову нового трикутника з такими ж розмірами.

2. Поворот та відображення: Рівні трикутники можуть бути отримані шляхом повороту або відображення вихідного трикутника. Ці операції
   не змінюють довжини сторін та кути трикутника, тому отримані трикутники залишаються рівними вихідному.

3. Практичне застосування: У геометрії та інженерії часто потрібна побудова рівних трикутників для різних завдань, таких як створення
   симетричних конструкцій чи перевірка правильності побудов.

4. Теорема про рівність трикутників: Існує кілька теорем, які допомагають визначити рівність трикутників, такі як теорема про рівність
   трикутників по трьох сторонах (SSS), по двох сторонах і кут між ними (SAS), і по двох кутах і стороні між ними (ASA).

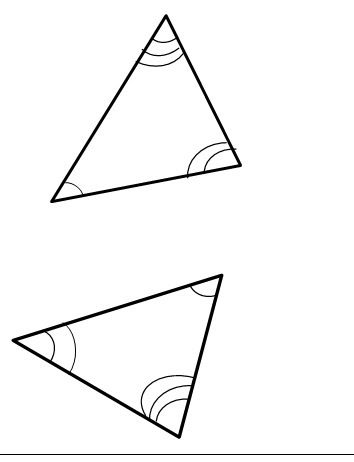
5. Кути та периметри рівних трикутників: У рівних трикутників проти відповідних сторін лежать рівні кути. На рисунку наведено рівні трикутники,
   але по-різному орієнтовані на площині. У рівних трикутників периметри також рівні.