Косинус кута

КОСИНУС КУТА (cos) - це відношення прилеглого катета прямокутного трикутника до гіпотенузі.

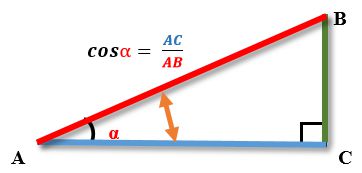
Косинус кута α позначається як  cos α.

Розглянемо по квадрантам зміни функції косинуса кута α при тому ж русі рухомого радіуса ОВ по колу по колу від 0° до 360°.

За визначенням косинуса кута: cos α = OC / OB. Для одиничної окружності, де ОВ=1, це довжина відрізка ОС. Отже, косинус кута - це величина проекції рухомого відрізка ОВ на вісь х.

Величина відрізка ОС змінюється (в межах кола) на осі х в залежності від положення рухомого радіуса (величини кута).

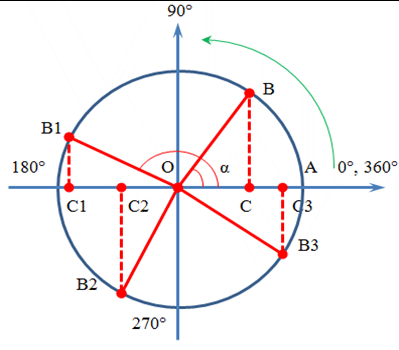
Розглянемо зміни функції (відрізка ОС) при русі рухомого радіуса окружності і збільшенні кута. Межі зміни косинуса кута будемо визначати по квадрантам.

У I квадранті (ОС):

при α = 0°  cos α = 1;

при 0° < α < 90° 1 > cos α > 0;

при α = 90° cos α = 0.

У II квадранті (ОС1):

при α = 90°  cos α = 0;

при 90° < α < 180° 0 > cos α  > -1;

при α = 180° cos α  = -1.

За пройдений рухомим радіусом (ОВ) перший півколо змінився від 1 до -1, найбільше і найменше його значення збігаються з довжиною радіусу на позитивній і негативній півосях х.

Друге півколо руху рухомого радіусу можна розглядати як позитивний напрям (при русі ОВ далі проти годинникової стрілки) і як негативне спрямування (якщо ОВ обертати за годинниковою стрілкою). Розглянемо тільки позитивний напрямок.

У III квадранті (ОС2):

при α = 180°  cos α = -1;

при 180° < α < 270° -1 <  cos α < 0;

при α = 270°  cos α = 0;

У IV квадранті (ОС3):

при α = 270°  cos α = 0;

при 270° < α < 360° 0 <  cos α < 1;

при α = 360°  cos α = 1.

За пройдене друге півколо змінився від -1 до 1, а найменше та найбільше його значення збігаються з довжиною радіусу на негативній та позитивній півосі х.

За весь оборот рухомого радіусу ОВ, від збігу з ОА до другого їх збігу, кут чисельно змінився від 0° до 360°, а чисельне значення косинуса кута змінювалося в межах від 1 до -1.

Чисельне значення синуса і косинуса кута залежить тільки від градусної міри кута і не залежить від параметрів прямокутного трикутника і його розташування на площині. Функції синуса і косинуса кута в чисельному значенні не перевищують ±1.

Обчислити значення синуса і косинуса будь-якого гострого кута прямокутного трикутника завжди можна, якщо відомі довжини його катетів і гіпотенузи, але частіше обчислення не виробляють, а зчитують значення функцій за таблицями логарифмів тригонометричних функцій в залежності від величини гострого кута.

Значення косинуса кута α