|
|
Правильний Тетраедр
Окремим випадком правильної трикутної піраміди є тетраедр.
Тетраедр - це правильний багатогранник (правильна трикутна піраміда) у якій всі грані є правильними трикутниками.
Характеристики тетраедра:
-
Усі грані рівні.
-
4 грані, 4 вершини та 6 ребер.
-
Усі двогранні кути при ребрах і всі тригранні кути при вершинах рівні.
Елементи тетраедра:
- Медіана тетраедра - це відрізок, що з'єднує вершину з точкою перетину медіан протилежної грані (медіан рівностороннього
трикутника, протилежного вершині).
- Бімедіана тетраедра - це відрізок, що з'єднує середини перехресних ребер (з'єднує середини сторін трикутника, що є однією
з граней тетраедра).
- Висота тетраедра - це відрізок, що з'єднує вершину з точкою протилежної грані та перпендикулярний цій грані (тобто є висотою,
проведеною від будь-якої грані, також збігається з центром описаного кола).
Властивості тетраедра:
-
Усі медіани та бімедіани тетраедра перетинаються в одній точці.
-
Ця точка ділить медіани у відношенні 3:1, рахуючи від вершини.
-
Ця точка ділить бімедіани навпіл.
Площа, обсяг, висота, радіус вписаної і описаної сфери і інші формули для тетраедра
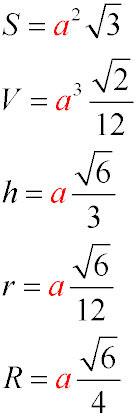
- a - довжина ребра тетраедра
- S - Площа поверхні. ( Формула 1)
- V - Об'єм: Об'єм тетраедра можна знайти за формулою 2.
- h - Висота тетраедра
- r - Радіус вписаної сфери Вписана сфера торкається всіх граней тетраедра в їх центрах. (Формула 4)
- R - Радіус описаної сфери: Описана сфера проходить через усі вершини тетраедра.(Формула 5)
Застосування тетраедра:
Тетраедр має широке застосування в різних галузях науки і техніки. Наприклад, у хімії тетраедрична структура є основою для багатьох молекул,
таких як метан (CH4). У математиці та геометрії тетраедр використовується для вивчення властивостей багатогранників та їх симетрій. У фізиці
тетраедричні структури зустрічаються в кристалічних решітках деяких матеріалів.
Див. приклади розв'язання задач: формули і властивості тетраедра.
Практичні приклади
Примітка. Це частина уроку із завданнями з геометрії (розділ стереометрія, завдання про піраміду).
Якщо Вам необхідно вирішити задачу геометрії, якої тут немає - пишіть про це у форумі.
У задачах замість символу "квадратний корінь" застосовується знак "√".
Завдання 1.
Знайдіть площу поверхні трикутної піраміди, у якої кожне ребро дорівнює √3
Рішення.
Оскільки всі ребра трикутної піраміди рівні – вона є правильною.
Площа поверхні правильної трикутної піраміди дорівнює S = a2√3 .
Тоді
S = 3√3
Відповідь: 3√3
Завдання.
Усі ребра правильної трикутної піраміди дорівнюють 4 см. Знайдіть об'єм піраміди
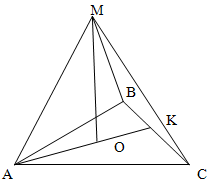
Рішення.
Оскільки у правильній трикутній піраміді висота піраміди проектується в центр основи,
який одночасно є центром описаного кола, то
AO = R = √3 / 3 a
AO = 4√3 / 3
Таким чином, висота піраміди OM може бути знайдена з прямокутного трикутника AOM
AO2 + OM2 = AM2
OM2 = AM2 - AO2
OM2 = 42 - ( 4√3 / 3 )2
OM2 = 16 - 16/3
OM = √(32/3)
OM = 4√2 / √3
Об'єм піраміди знайдемо за формулою V = 1/3 Sh
При цьому площу основи знайдемо за формулою S = √3/4 a2
V = 1/3 (√3 / 4 * 16 ) ( 4√2 / √3 )
V = 16√2 / 3
Відповідь: 16√2 / 3 см
Об'єм правильної трикутної піраміди |
Описание курса
| Піраміда з прямокутним трикутником в основі
|

