|
|
Правильна чотирикутна призма
Визначення.
Правильна чотирикутна призма - це шестигранник, підставами якого є два рівних квадрата, а бічні грані є рівні прямокутники
Бічне ребро - це загальна сторона двох суміжних бічних граней
Висота призми - це відрізок, перпендикулярний основам призми
Діагональ призми - відрізок, що з'єднує дві вершини основ, які не належать до однієї грані
Діагональна площина - площина, яка проходить через діагональ призми і її бічні ребра
Діагональний перетин - межа перетину призми і діагональної площині. Діагональний перетин правильної чотирикутної призми є прямокутником
Перпендикулярний перетин (ортогональний перетин) - це перетин призми і площини, проведеної перпендикулярно її бічним ребрам
Елементи правильної чотирикутної призми
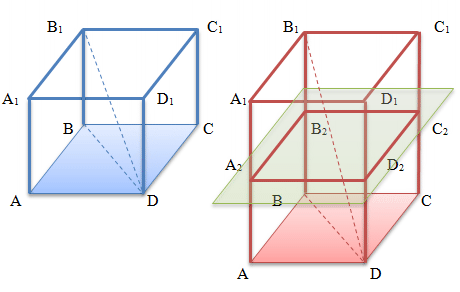
На малюнку зображено дві правильні чотирикутні призми, у яких позначені відповідними буквами:
- Основи ABCD та A1B1C1D1 якi рівні і паралельні один одному
- Бічні грані AA1D1D, AA1B1B, BB1C1C та CC1D1D, кожна з яких є прямокутником
- Бічна поверхня - сума площ всіх бічних граней призми
- Повна поверхня - сума площ всіх основ і бічних граней (сума площі бічної поверхні і основ)
- Бічні ребра AA1, BB1, CC1 та DD1.
- Дiагональ B1D
- Дiагональ основи BD
- Діагональний перетин BB1D1D
- Перпендикулярний перетин A2B2C2D2 .
Властивості правильної чотирикутної призми
- Основами є два рівних квадрата
- Основи паралельні один одному
- Бічними гранями є прямокутники
- Бічні грані рівні між собою
- Бічні грані перпендикулярні основам
- Бічні ребра паралельні між собою і дорівнюють одне одному
- перпендикулярний перетин є перпендикулярним всім бічним ребрам і є паралельним основанням
- Кути перпендикулярного перетину - прямі
- Діагональний перетин правильної чотирикутної призми є прямокутником
- Перпендикулярний (ортогональний перетин) паралельний основам
Формули для правильної чотирикутної призми
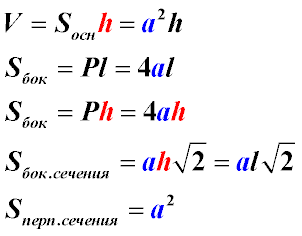
Вказівки до вирішення завдань
При вирішенні завдань на тему "правильна чотирикутна призма" мається на увазі, що:
Правильна призма - призма в основі якої лежить правильний багатокутник, а бічні ребра перпендикулярні площинам основи. Тобто правильна чотирикутна призма містить в своєму основанні квадрат. (Див. вище "властивості правильної чотирикутної призми")
Примітка. Це частина уроку з завданнями по геометрії (розділ стереометрія - призма). Тут розміщені завдання, які викликають труднощі при вирішенні. Якщо Вам необхідно вирішити задачу з геометрії, якої тут немає - пишіть про це в форумі. Для позначення дії добування квадратного кореня в рішеннях задач використовується символ √ .
Завдання
У правильної чотирикутної призмі площа основи 144 см2, а висота 14 см. Знайти діагональ призми і площу повної поверхні.
Рішення.
Правильний чотирикутник - це квадрат.
Відповідно, сторона основи буде дорівнювати √144 = 12 см.
Звідки діагональ основи правильної прямокутної призми дорівнюватиме
√( 122 + 122 ) = √288 = 12√2
Діагональ правильної призми утворює з діагоналлю основи і висотою призми прямокутний трикутник. Відповідно, по теоремі Піфагора діагональ заданої правильної чотирикутної призми дорівнюватиме
√( ( 12√2 )2 + 142 ) = 22 см
Відповідь: 22 см
Завдання
Визначте повну поверхню правильної чотирикутної призми, якщо її діагональ дорівнює 5 см, а діагональ бічної грані дорівнюють 4 см.
Рішення.
Оскільки в основі правильної чотирикутної призми лежить квадрат, то сторону основи (позначимо як a) знайдемо по теоремі Піфагора:
a2 + a2 = 52
2a2 = 25
a = √12,5
Висота бічної грані (позначимо як h) тоді буде дорівнювати:
h2 + 12,5 = 42
h2 + 12,5 = 16
h2 = 3,5
h = √3,5
Площа повної поверхні буде дорівнювати сумі площі бічної поверхні і подвоєної площі основи
S = 2a2 + 4ah
S = 25 + 4√12,5 * √3,5
S = 25 + 4√43,75
S = 25 + 4√(175/4)
S = 25 + 4√(7*25/4)
S = 25 + 10√7 ≈ 51,46 см2 .
Відповідь: 25 + 10√7 ≈ 51,46 см2 .
Пряма призма |
Описание курса
| Призма з трикутником в основі
|

