|
|
См. також биссектриса угла.
Бісектриса кута трикутника
Бісектриса трикутника - відрізок бісектриси кута, що з'єднує вершину цього кута з точкою на протилежній стороні.
У биссектрис кута трикутника є маса властивостей, які описуються через властивості трикутника. Це допоможе у вирішенні завдань.
Властивості биссектрис трикутника
-
Бісектриса трикутника, проведена з даної вершини, тотожна бісектрисі відповідного кута. Бісектриса кута трикутника, що виходить з його вершини, ділить цей кут трикутника навпіл
-
Всі три бісектриси трикутника перетинаються в одній точці, яка розташована завжди в площині трикутника і є центром вписаного кола. Примітка. Маються на увазі бісектриси внутрішніх кутів трикутника.

- Кожна бісектриса трикутника ділиться точкою перетину биссектрис щодо суми прилеглих сторін до протилежної, починаючи з вершини

- Бісектриса будь-якого внутрішнього кута трикутника ділить протилежну сторону на частини, пропорційні сторонам трикутника
- Бісектриси одного внутрішнього і двох зовнішніх кутів трикутника перетинаються в одній точці. Ця точка - центр однієї з трьох вневпісанних кіл цього трикутника.
- Кут між биссектрисами двох суміжних кутів (між внутрішніми і зовнішніми биссектрисами кутів трикутника при одній вершині) дорівнює 90 градусам
-
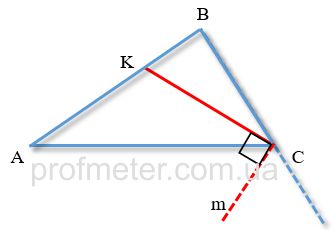
Властивості биссектрис рівнобедреного трикутника
-
У рівнобедреного трикутника медіана, бісектриса і висота, проведені до основи трикутника, збігаються
-
Якщо в трикутнику дві бісектриси рівні, то трикутник - рівнобедрений (теорема Штейнера - ЛЕМУС), і третя бісектриса одночасно є медіаною і висотою того кута, з якого вона виходить.
-
У трикутник дві бісектриси рівні, а третя бісектриса є його медіаною і висотою
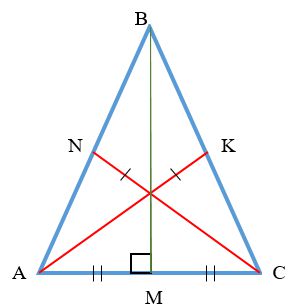
Властивості биссектрис рівностороннього трикутника
-
У рівностороннього трикутника всі три бісектриси зовнішніх кутів паралельні протилежним сторонам
-
У рівностороннього трикутника всі три «чудові» лінії (висота, бісектриса і медіана) збігаються і три «чудових» точки (точки ортоцентра, центру ваги і центру вписаного і описаного кіл) знаходяться в одній точці перетину «чудових» ліній, тобто теж збігаються
-
У рівностороннього трикутника всі три внутрішні бісектриси рівні
Формули знаходження бісектриси кута
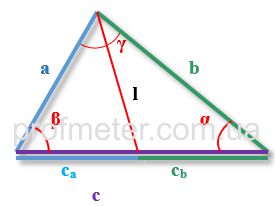
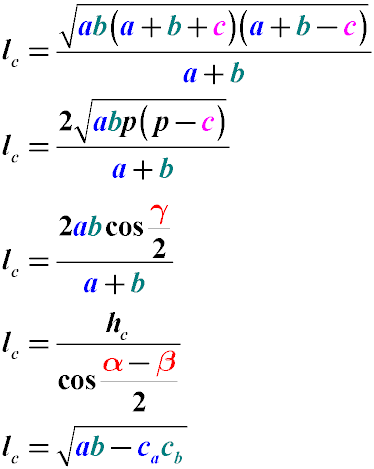
a, b, c - сторони трикутника, при цьому бісектриса проведена з кута, що знаходиться між сторонами a, b
α, β, γ - кути трикутника, протилежні боки a, b, c відповідно
p - напівпериметр трикутника (половина суми всіх його сторін)
ca, cb - відрізки, на які биссектрисой, проведеної з кута c розбита сторона c
lc - довжина бісектриси, проведеної до сторони c з кута γ.
Довжина биссектрис трикутника може бути виражена через рівність з квадратом суми всіх його сторін.

Формули знаходження відстані від кута до точки перетину биссектрис
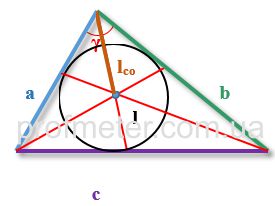
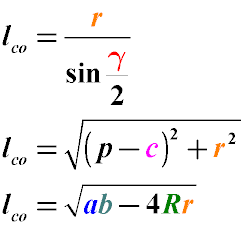
где
lco - довжина відрізка, що лежить на бісектрисі від вершини кута до центру перетину биссектрис
r -радіус кола, вписаного в трикутник
R - радіус описаного кола
a, b, c - сторони трикутника, при цьому бісектриса проведена з кута, що знаходиться між сторонами a, b
γ - кут трикутника, протилежний стороні c
p - напівпериметр трикутника (половина суми всіх його сторін)
Завдання про доказ рівності кутів на підставі властивостей бісектриси.
Примітка. В даному уроці викладені завдання з геометрії про бісектрисі. Якщо Вам необхідно вирішити задачу з геометрії, якої тут немає - пишіть про це на форумі. Майже напевно курс буде доповнений.
Луч AD є бісектрисою кута A. На сторонах кута A відзначені точки B, C так що кут ADC дорівнює куту ADB.
Довести, що AB = AC.
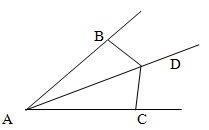
Рішення.
Розглянемо трикутники ADB і ADC. Сторона AD у них загальна, кути DAC і DAB рівні, так як бісектриса AD ділить кут А навпіл, а кути ADC і ADB рівні за умовою задачі.
Таким чином, трикутники ADB і ADC рівні по стороні і двом кутам.
Отже AB = AC.
Бісектриса кута |
Описание курса
| Площа геометричної фігури
|

