Синус, косинус і тангенс кута 15 градусів

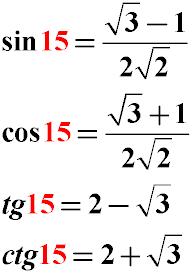
Як знайти значення тригонометричних функцій для кута 15 градусів

Знайдемо значення синуса, косинуса і тангенса для кута 15 градусів аналітичним способом.
На перший погляд, знаходження значень синуса, косинуса і тангенса для кута 15 градусів - завдання складне. Однак, це не зовсім так.
Нам на допомогу прийдуть формули перетворення подвійного кута тригонометричних функцій..

Справа в тому, що ми можемо уявити кут в 30 градусів, як подвійний кут 15 градусів ( 2 * 15 ).

Тоді, відштовхуючись від тотожності:
cos 2α = 1 - 2sin²α

Приймаємо подвійний кут як 2 * 15 градусів, тоді
cos 30 = 1 - 2sin²15
sin²15 = ( 1 - cos 30 ) / 2

Значення косинуса для кута 30 градусів легко обчислити. Воно дорівнює √3/2
sin²15 = ( 1 - √3/2 ) / 2
sin 15 = √ (( 1 - √3/2 ) / 2 )
верхню частину дробу під коренем приведемо до спільного знаменника (2)
sin 15 = √ ((  (2 - √3) /2 ) / 2 ) = √(  (2 - √3) / 4 )
тепер у нас одна дріб під знаком кореня. Помножимо чисельник і знаменник на два
sin 15 = √(  (2 - √3) / 4 ) = √( (4 - 2√3) / 8 )
найцікавіший момент, ми можемо уявити 4 - 2√3 як (√3-1)²
тоді
sin 15 = √( (√3-1)² / 8 ) = (√3-1)/ √8 = (√3-1)/ (2√2)

шляхом нескладних агебраіческіх перетворень отримуємо:

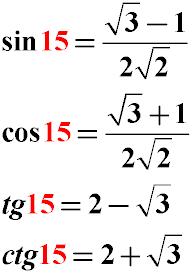
Як видно з прикладу, значення тригонометричних функцій кутів синуса, косинуса і тангенса 15 градусів можуть бути отримані шляхом нескладних тригонометричних перетворень з використанням тригонометричних тотожностей перетворень подвійних кутів і половин заданих кутів.

Див. Також повну таблицю значень тригонометричних функцій (таблицю синусів, косинусів і тангенсів).

Нижче наведені також значення тригонометричних функцій для кута 15 градусів у вигляді десяткового дробу з чотирма знаками після коми.

π/12	синус 15  sin 15	косинус 15 cos 15	тангенс 15 tg 15	котангенс 15 ctg 15
Значення	0.2588190451	0.96592582628	0.26794919243	3.73205080757