|
|
Завдання
В основі піраміди лежить прямокутний трикутник, один із катетів якого 8см, а радіус описаного біля нього кола дорівнює 5 см.
Основою висоти цієї піраміди є середина гіпотенузи. Висота піраміди дорівнює 12см. Обчислити бічні ребра піраміди.
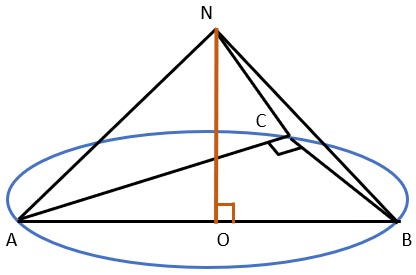
Рішення.
В основі піраміди лежить прямокутний трикутник. Центр кола, описаного біля прямокутного трикутника, лежить на його гіпотенузі.
Відповідно, AB = 10 см, AO = 5 см.
Оскільки висота ON = 12 см, то величина ребер AN та NB дорівнює
AN2 = AO2 + ON2
AN2 = 52 + 122
AN = √169
AN = 13
Оскільки в прямокутному трикутнику гіпотенуза є одночасно діаметром описаного кола,
а OC одночасно також буде радіусом описаного кола, то
Оскільки нам відома величина AO = OB = 5 см і величина одного з катетів основи (8 см), то висота, опущена на гіпотенузу,
дорівнюватиме
AB = 2R = 10
R = 5
CO = 5 см
Відповідно, величина ребра CN дорівнюватиме
CN2 = CO2 + NO2
CN2 = 25 + 144
CN = √169
Відовідь: 13, 13 , 13
Завдання
Основа піраміди прямокутний трикутник, катети якого дорівнюють 8 і 6 см. висота піраміди дорівнює 10 см.
Обчислити обсяг піраміди.
Рішення.
Об'єм піраміди знайдемо за формулою:
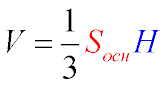
Площу основи знайдемо за формулою знаходження площі прямокутного трикутника:
S = ab/2 = 8 * 6 / 2 = 24
звідки
V = 1/3 * 24 *10 = 80 см3 .
Тетраедр |
Описание курса
| Правильна піраміда
|

