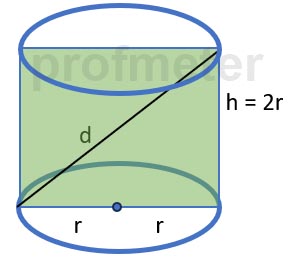
Завдання. Осьовий переріз циліндра - квадрат, діагональ якого дорівнює 4 см. Знайдіть об'єм циліндра

1. Знайти довжину сторони квадратного перерізу:

   • Діагональ квадрата дорівнює 4 см.
   • Для квадрата співвідношення між довжиною сторони a і діагоналлю d визначається формулою:


• Розв'язуючи для a:
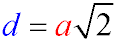
a = d / √2= 4 / √2 = 2√2 cm
2. Визначити радіус циліндра:
   • Довжина сторони квадрата дорівнює діаметру основи циліндра.
   • Отже, радіус rr циліндра:
r = a / 2 = 2√2 / 2 = √2 см
3. Знайти висоту циліндра:
   • Висота h циліндра дорівнює довжині сторони квадратного перерізу:
h=2√2 см
4. Обчислити об'єм циліндра:
   • Об'єм V циліндра визначається формулою:


• Підставляючи значення:

Таким чином, об'єм циліндра становить 4√2π см³.

Задача

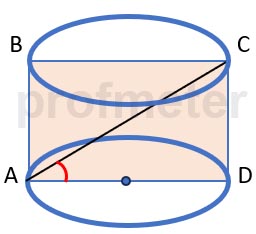
Знайдіть площу повної поверхні циліндра, якщо діагональ його осьового перерізу, яка дорівнює 8 см,
утворює з утворюючою циліндра кут величиною 30 градусів.

Рішення

Циліндр має осьовий переріз у вигляді паралелограма з вказаним кутом діагоналі.

Оскільки AC = 8 см, а кут ACD = 30°, то:

Пояснення: Трикутник ACD є прямокутним. Відповідно, CD / AC = cos⁡(∠ACD) за властивістю тригонометричних функцій
у прямокутному трикутнику. Значення cos⁡(30°) можна знайти з таблиці значень тригонометричних функцій.

Аналогічно,

З цього радіус основи циліндра дорівнює:

Площа основи циліндра:

Площа бічної поверхні циліндра дорівнює площі його розгортки - добутку довжини кола основи і висоти циліндра. Тобто:

Загальна площа поверхні циліндра:

Відповідь: 4π +  16π√3