Шестикутник - це багатокутник, загальна кількість кутів (вершин) якого дорівнює шести.

Випуклий шестикутник - це багатокутник, із загальною кількістю вершин, що дорівнює шести, при цьому всі точки
такого шестикутника лежать по одну сторону від прямої, яка проведена між двома будь-якими сусідніми його вершинами.

При розв'язанні задач для знаходження площі довільного (неправильного) шестикутника використовують метод трапецій,
який полягає в розбиття фігури на окремі трапеції, площу кожної з яких можна знайти за всіма відомими формулами.

Правильний шестикутник

Властивості правильного шестикутника

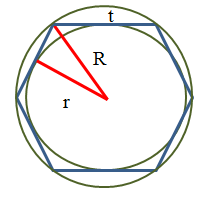
всі внутрішні кути рівні між собою  кожен внутрішній кут правильного шестикутника дорівнює 120 градусам  всі сторони рівні між собою сторона правильного шестикутника дорівнює радіусу описаного кола  правильний шестикутник заповнює плоскість без пропусків і накладень

Формули для правильного шестикутника

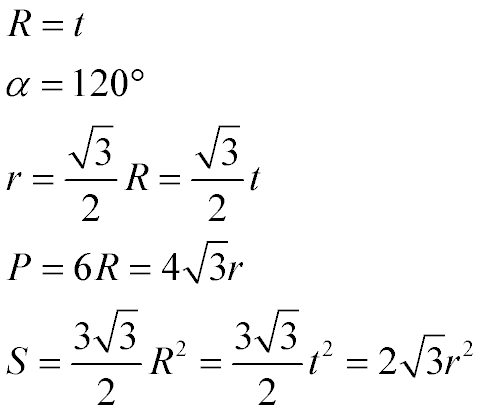
(По порядку розташування формул)

• Радіус описаного кола (R) правильного шестикутника дорівнює його стороні (t)

• Усі внутрішні кути дорівнюють 120 градусам

• Радіус вписаного кола (r) дорівнює кореню з трьох, поділеному на два і помноженому на довжину сторони t 

• (радіус описаного кола R)

• Периметр правильного шестикутника (P) дорівнює шести радіусам описаного кола (R) або чотири корені з трьох, 

• помноженим на радіус вписаного кола (r)

• Площа правильного шестикутника дорівнює трьом корінням з трьох навпіл, помноженим на квадрат радіусу
  описаного кола (R) або квадрат сторони (t); або площа правильного шестикутника дорівнює двом корінням з трьох,
  помноженим на квадрат радіусу вписаного кола (t)

Завдання