Завдання 1. Знайти об'єм піраміди
Діагональ основи правильної чотирикутної піраміди дорівнює 4 см, а бічна грань утворює з основою кут 60 градусів.
Знайдіть об'єм піраміди.
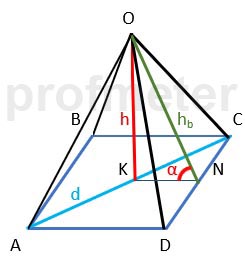
Розв'яжемо задачу крок за кроком:
-
Знайдемо сторону основи піраміди:
-
Основою правильної чотирикутної піраміди є квадрат.
-
Діагональ квадрата d пов'язана зі стороною aa формулою: d=a√2
-
Діагональ d = 4 см, отже:
4 = a√2 ⟹ a = 4 / √2 =2√2 см
- Знайдемо висоту бічної грані піраміди:
-
Висота бічної грані hb утворює з основою кут 60 градусів.
-
Висота бічної грані hb є гіпотенузою прямокутного трикутника, де одна з катетів дорівнює половині сторони основи a/2,
а інша катета - висота піраміди h.
-
Використовуємо тригонометричну функцію косинуса:
cos 60°=( a/2 ) / hb
1/2=2√2/2 / hb
hb= 2√2
- Знайдемо висоту піраміди:
-
Використовуємо тригонометричну функцію синуса:
sin60°=h / hb
√3/2 = h / 2√2
h = 2√2⋅ √3/2 =√6 см
- Знайдемо об'єм піраміди:
-
Об'єм піраміди V обчислюється за формулою:
V=1 / 3 Sосн⋅h
-
Площа основи Sосн квадрата зі стороною a=2√2:
Sосн=(2√2)2=8 см2
V=1 / 3 ⋅ 8 ⋅ √6 = 8 √6 / 3 см3
Відповідь: Обсяг піраміди дорівнює 8√6 / 3 см³.
Завдання 2
Сторона основи правильної чотирикутної піраміди дорівнює a. Двогранні кути при основі дорівнюють α.
Знайти площу повної поверхні піраміди.
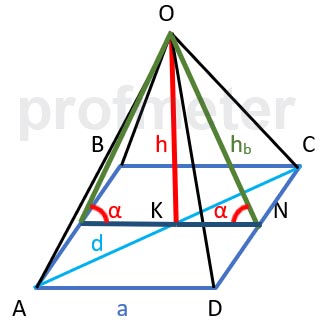
Рішення:
Щоб знайти площу повної поверхні правильної чотирикутної піраміди, потрібно знайти площу її основи та площу всіх бічних граней.
-
Площа основи: Основою правильної чотирикутної піраміди є квадрат зі стороною aa. Площа квадрата обчислюється за формулою:
Sоснови = a2
-
Площа бічних граней: Кожна бічна грань правильної чотирикутної піраміди є рівнобедреним трикутником. Висота цих трикутників
опускається з вершини піраміди на середину сторони основи. Позначимо висоту трикутника як hb.
Висоту hb можна знайти за допомогою двогранного кута α при основі. Висота трикутника буде дорівнювати:
hb = a / 2⋅cos(α)
Площа одного трикутника обчислюється за формулою:
Sтрикутника=1/2⋅a⋅hb=1 / 2⋅a⋅( a / 2⋅cos(α) )=a2⋅cos(α) / 4
Оскільки піраміда має чотири бічні грані, загальна площа бічних граней буде:
Sбічних=4⋅Sтрикутника=4⋅a2⋅cos(α) / 4= a2⋅cos(α)
-
Площа повної поверхні: Площа повної поверхні піраміди дорівнює сумі площі основи та площі бічних граней:
Sповна=Sоснови+Sбічних=a2+a2⋅cos(α)=a2(1+cos(α))
Отже, площа повної поверхні правильної чотирикутної піраміди дорівнює a2(1+cos(α))
Правильна піраміда з чотирикутником в основі |
Описание курса
| Знаходження кутів правильної чотирикутної піраміди
|

