|
Примітка. Це частина уроку із завданнями з геометрії (розділ паралелограм). Якщо Вам необхідно вирішити
задачу з геометрії, якої тут немає - пишіть про це у форумі.
Див. також: Властивості та площа паралелограма.
Висота паралелограма - формули і властивості
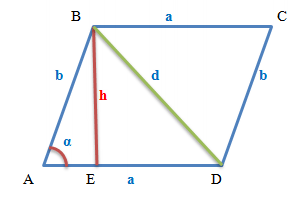
Позначення у формулах еквівалентні позначенням на малюнках, а саме:
а - сторони, паралелограма, паралельні один одному
b - бічні сторони паралелограма
h - висота паралелограма
d - дiагональ паралелограма
S - площа паралелограма
α - гострий кут при основі паралелограма
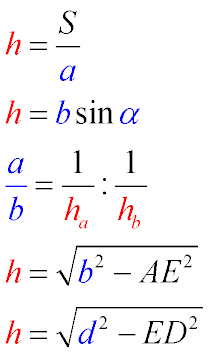
Висота паралелограма дорівнює співвідношенню площі до основи (Формула 1)
Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2)
Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот,
опущених на відповідні сторони (Формула 3)
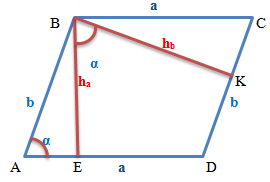
Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при
сусідній вершині (Малюнок 2)
Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка,
створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4)
Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата
довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5)
Завдання
Висота паралелограма проведена з вершини тупого кута і дорівнює 5 см. Висота поділяє сторону паралелограма навпіл.
Гострий кут дорівнює 30 градусів. Знайдіть діагональ паралелограма, проведену з вершини тупого кута та кути, які вона
утворює зі сторонами паралелограма.
Рішення.
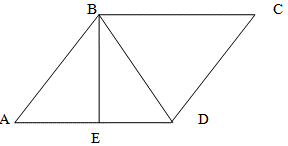
Оскільки, за умовою задачі, AE=ED, то трикутники ABE та DBE рівні між собою (за першою ознакою рівності трикутників:
рівні дві сторони та кут між ними, AE=ED та BE – загальна сторона, а BE утворює з AD кут 90 градусів ). Таким чином,
кут ADB дорівнює 30 градусів. Відповідно, кут DBC також дорівнює 30 градусам як внутрішній навхрест лежачий при
паралельних прямих BC і AD.
З прямокутного трикутника ABE визначимо, що кут ABE дорівнює 180 – 90 – 30 = 60 градусів. Звідки (з рівності трикутників
ABE та DBE) кут EBD також дорівнює 60 градусів. Таким чином, діагональ утворює з другою основою кут
ABD = 60 + 60 = 120 градусів. BDC = ABD = 120 градусів як внутрішній навхрест лежачий.
Знайдемо довжину діагоналі.
BE / BD = cos ∠EBD
BE / BD = cos 60
Підставимо значення косинуса 60 градусів і отримаємо:
BE/BD = 1/2
За умовою задачі BE = 5 см, звідки
5/BD = 1/2
BD = 10
Відповідь: довжина діагоналі паралелограма дорівнює 10 см, кути, які утворює діагональ з основами дорівнюють
30 і 120 градусів.
Паралелограм |
Описание курса
| Багатокутники
|

