|
|
Примітка. В даному уроці викладені завдання з геометрії про медіані трикутника. Якщо Вам необхідно вирішити задачу з геометрії, якої
тут немає - пишіть про це в форумі. Майже напевно курс буде доповнений.
Завдання. Знайти довжину медіани трикутника через його сторони
Сторони трикутника дорівнюють 8, 9 і 13 сантиметрів. До найбільшої стороні трикутника проведена медіана. Визначте медіану трикутника,
виходячи з розмірів його сторін.
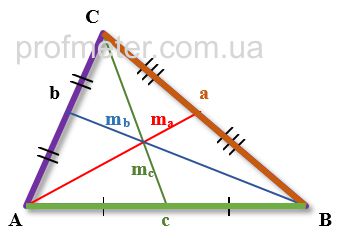
Рішення.
Завдання має два способи вирішення. Перший, який не подобається вчителям середньої школи, але є найбільш універсальним.
Спосіб 1.
Застосуємо теорему Стюарта, згідно з якою квадрат медіани дорівнює одній четвертій від суми подвоєних квадратів сторін з якої відняли
квадрат боку, до якої проведена медіана.
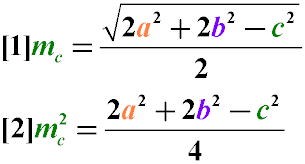
mc2 = (2a2 + 2b2 - c2) / 4
відповідно
mc2 = (2 * 82 + 2 * 92 - 132) / 4
mc2 = 30,25
mc = 5,5 см
Спосіб 2.
Другий спосіб вирішення, який викладачі в школі люблять - це додаткові побудови трикутника до паралелограма і рішення через теорему про
діагоналі паралелограма.
Продовжимо сторону трикутника ABC і медіану BO добудувавши їх до паралелограма. В цьому випадку медіана BO трикутника ABC буде
дорівнювати половині діагоналі отриманого паралелограма, а дві сторони трикутника AB, BC - його бічним сторонам. Третя сторона трикутника AC,
до якої була проведена медіана, є другою діагоналлю отриманого паралелограма.
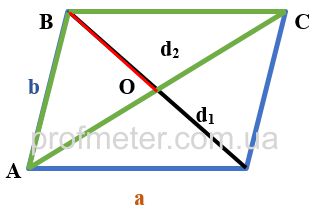
Згідно з теоремою, сума квадратів діагоналей паралелограма дорівнює подвоєної сумі квадратів його сторін.
2 (a2 + b2) = d12 + d22
Позначимо діагональ паралелограма, яка утворена продовженням медіани вихідного трикутника як х, отримаємо:
2 (82 + 92) = 132 + x2
290 = 169 + x2
x2 = 290 - 169
x2 = 121
х = 11
Оскільки шукана медіана дорівнює половині діагоналі паралелограма, то величина медіани трикутника складе 11/2 = 5,5 см
Відповідь: 5,5 см
Медіана трикутника |
Описание курса
| Кут між висотою і медіаною трикутника
|

