Визначення чотирикутника
Чотирикутник - це багатокутник з чотирма вершинами, три з яких не лежать на одній прямій.
Чотирикутник - це геометрична фігура, що складається з чотирьох точок, три з яких не лежать на одній прямій, послідовно з'єднана відрізками.
Властивості чотирикутника
Чотирикутник може бути:
- Самоперетинаючим
- Неопуклим
- Опуклим

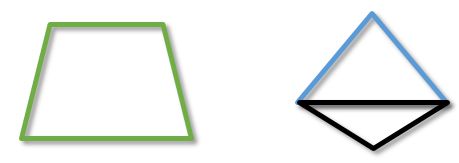
Самоперетинаючий чотирикутник - це чотирикутник, у якого будь-які з його сторін мають точку перетину (на малюнку синім кольором).
Неопуклий чотирикутник - це чотирикутник, у якому один з внутрішніх кутів більше 180 градусів (на малюнку позначено червоним кольором)
Сума кутів будь-якого чотирикутника, який не є самоперетинаючим завжди дорівнює 360 градусів.
Особливі види чотирикутників
Чотирикутники можуть мати додаткові властивості, утворюючи особливі види геометричних фігур:
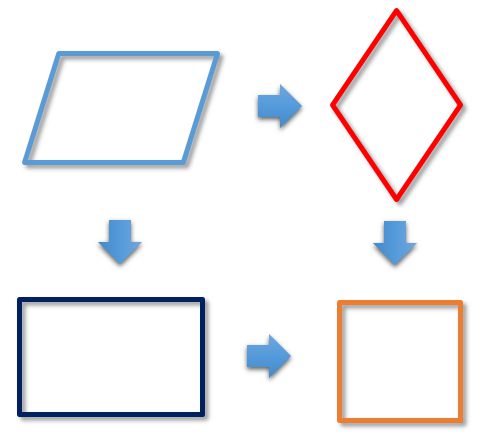
Детальніше про кожного з особливих видів чотирикутника можна дізнатися, перейшовши за посиланнями вище.
Як видно з малюнка, особливі види чотирикутників успадковують властивості своїх "предків". Наприклад, прямокутник (на малюнку показаний темно-синім кольором) є особливим випадком паралелограма (на малюнку показаний блакитним кольором). Таким чином, у нього зберігаються всі його властивості та додаються свої, особливі. Тому при вирішенні задач про прямокутники можна застосовувати всі властивості і теореми паралелограма.
Квадрат (на малюнку показаний помаранчевим кольором) - окремий випадок прямокутника. Тобто квадрат має всі властивості паралелограма, прямокутника, а також і свої, особливі. Але, найцікавіше, квадрат також є окремим випадком ромба (на малюнку показаний червоним кольором), тобто, крім зазначених (паралелограм, прямокутник), він має ще й всі властивості ромба.
Також, цікавими особливими випадками чотирикутника є трапецiя и дельтоiд.
Чотирикутник і коло
Чотирикутник, описаний навколо кола (коло, вписане в чотирикутник).
Головна властивість описаного чотирикутника:
Чотирикутник можна описати навколо кола тоді і тільки тоді, коли суми довжин протилежних сторін рівні.
Чотирикутник, вписаний в коло (коло, описане навколо чотирикутника)
Головна властивість вписаного чотирикутника:
Чотирикутник можна вписати в коло тоді і тільки тоді, коли суми протилежних кутів дорівнюють 180 градусів.
Властивості довжин сторін чотирикутника
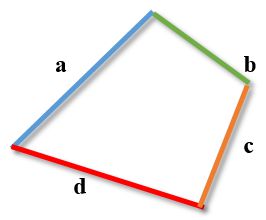
Модуль різниці будь-яких двох сторін чотирикутника не перевищує суми двох інших його сторін.
|a -b| ≤ c + d
|a -c| ≤ b + d
|a -d| ≤ b + c
|b -c| ≤ a + d
|b -d| ≤ a + b
|c -d| ≤ a + b
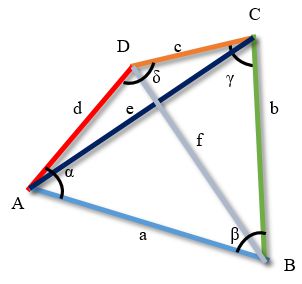
Важливо. Нерівність є вірною для будь-якої комбінації сторін чотирикутника. Малюнок наведено виключно для полегшення сприйняття.
У будь-якому чотирикутнику сума довжин трьох його сторін не менше довжини четвертої сторони.
a ≤ b + c + d
b ≤ a + c + d
c ≤ a + b + d
d ≤ a + b + c
Важливо. При вирішенні завдань в межах шкільної програми можна використовувати суворе нерівність (<). Рівність досягається тільки в разі, якщо чотирикутник є "виродженим", тобто три його точки лежать на одній прямій. Тобто ця ситуація не підпадає під класичне визначення чотирикутника.
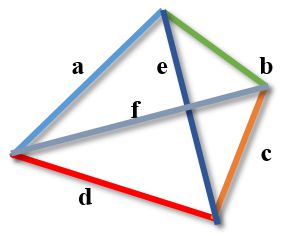
Співвідношення сторін і діагоналей може бути виражено формулою
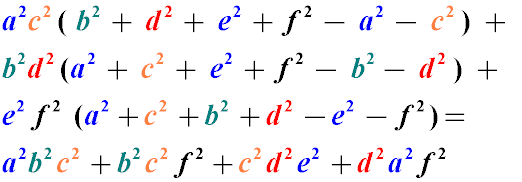
Нерiвнiсть Птолемея
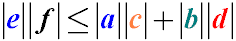
Твір довжин діагоналей чотирикутника менше або дорівнює сумі творів протилежних сторін чотирикутника.
Теорема Ґауса
Якщо в чотирикутнику дві пари протилежних сторін не паралельні, то дві середини його діагоналей лежать на прямій, яка проходить через середину відрізка, що з'єднує дві точки перетину діагоналей і точку перетину цих двох пар протилежних сторін.
Співвідношення Бретшнайдера
Твір квадратів діагоналей довільного несамоперетинаючого чотирикутника дорівнює сумі творів квадратів його протилежних сторін мінус подвоєний добуток всіх його сторін, яке помножене на косинус суми двох протилежних кутів.
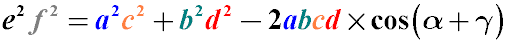
Формула Эйлера
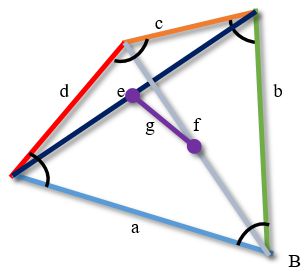
Квадрат подвійноï відстані між центрами діагоналей довільного несамоперетинаючого чотирикутника дорівнює сумі квадратів його сторін мінус сума квадратів його діагоналей
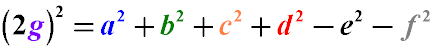
Середні лінії чотирикутника
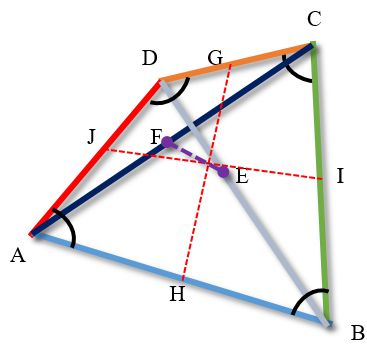
У кожного чотирикутника є три середні лінії.
Середніми лініями несамоперетинаючого чотирикутника називаються відрізки, що з'єднують середини його протилежних сторін (перша і друга) і відрізок, що з'єднує середини його діагоналей.
На малюнку середні лінії чотирикутника відзначені пунктирними лініями.
Центроїд чотирикутника
Центроїдом чотирикутника називається точка перетину всіх його середніх ліній.
Узагальнена теорема Ньютона
Середні лінії несамоперетинаючого чотирикутника, утворені центрами протилежних сторін (перша і друга середня лінія) і відрізком, що з'єднує середини діагоналей (третя середня лінія) перетинаються в одній точці і діляться нею навпіл.
Пряма, що проходить через середини діагоналей чотирикутника і його центр ваги також називається прямою Ньютона.
(див. Малюнок вище)
Теорема Вариньона
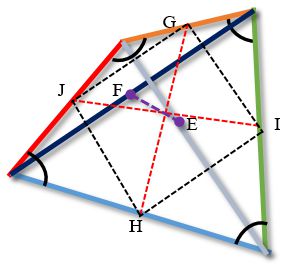
Чотирикутники, які утворюються відрізками, що з'єднують середини протилежних сторін (GIHJ), а також середини діагоналей чотирикутника і середини протилежних сторін (EHFG, JEIF) є паралелограми.
Ці паралелограми називаються паралелограми Варіньона.
Чотирикутник, утворений центрами протилежних сторін (на малюнку позначено пунктирною лінією GIHJ) називається великим паралелограмом Варіньона.
- Центри всіх трьох паралелограмів Варіньона лежать на середині відрізка, що з'єднує середини сторін вихідного чотирикутника (в цій же точці перетинаються відрізки, що з'єднують середини протилежних сторін - діагоналі варіньоновского паралелограма).
- Периметр великого паралелограма Варіньона дорівнює сумі діагоналей вихідного чотирикутника.
- Площа великого паралелограма Варіньона дорівнює половині площі вихідного чотирикутника
- Площа вихідного чотирикутника дорівнює добутку першої і другої середніх ліній чотирикутника на синус кута між ними
- Сума квадратів трьох середніх ліній чотирикутника дорівнює чверті суми квадратів всіх його сторін і діагоналей
Медіана прямокутного трикутника |
Описание курса
| Існування чотирикутника з сторонами заданої довжини
|

