Площа трикутника

Нижче наведені формули знаходження площі довільного трикутника, які підійдуть для знаходження площі будь-якого трикутника, незалежно від його властивостей, кутів або розмірів. Формули представлені у вигляді картинки, тут же наведені пояснення щодо застосування або обґрунтування їх правильності. Також, на окремому малюнку вказані відповідності літерних позначень у формулах і графічних позначень на кресленні.

Примітка. Якщо ж трикутник має особливі властивості (рівнобедрений, прямокутний, рівносторонній), можна використовувати формули, наведені нижче, а також додатково спеціальні, вірні тільки для трикутників з даними властивостями, формули:  

• "Формули площі рівнобедреного трикутника"
• "Формули площі прямокутного трикутника"
• "Формули площі равносторонього трикутника"

  

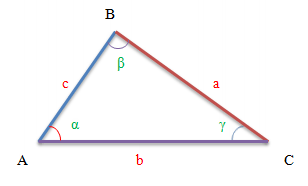
Формули площi трикутника

    

Пояснення до формул:

a, b, c - довжини сторін трикутника, площу якого ми хочемо знайти;
r - радіус вписаного в трикутник кола;
R - радіус описаного навколо трикутника кола;
h - висота трикутника, що опущена на сторону;
p - напівпериметр трикутника, 1/2 суми його сторін (периметра);
α - кут, протилежний стороні a трикутника;
β - кут, протилежний стороні b трикутника;
γ - кут, протилежний стороні c трикутника;
ha, hb, hc - висота трикутника, що опущена на сторону a, b, c;
відповідно.

Зверніть увагу, що наведені позначення відповідають малюнку, який знаходиться вище, щоб при вирішенні реального завдання з геометрії Вам візуально було легше підставити в потрібні місця формули правильні значення.

• Площа трикутника дорівнює половині твору висоти трикутника на довжину сторони, на яку ця висота опущена (Формула 1). Правильність цієї формули можна зрозуміти логічно. Висота, опущена на основу, розіб'є довільний трикутник на два прямокутних. Якщо добудувати кожен з них до прямокутника з розмірами b і h, то, стає зрозуміло, що, площа даних трикутників буде дорівнювати рівно половині площі прямокутника (Sпр = bh).
• Площа трикутника дорівнює половині добутку двох його сторін на синус кута між ними (Формула 2). (див. Приклад рішення задачі з використанням цієї формули нижче). Незважаючи на те, що вона не здається схожою на попередню, вона легко може бути в неї перетворена. Якщо з кута B опустити висоту на сторону b, виявиться, що твір боку a на синус кута γ за властивостями синуса в прямокутному трикутнику дорівнює проведеній нами висоті трикутника, що і дасть попередню формулу.
• Площа довільного трикутника може бути знайдена через твір половини радіуса вписаного в нього кола на суму довжин усіх його сторін (Формула 3), простіше кажучи, потрібно напівпериметр трикутника помножити на радіус вписаного кола (так легше запам'ятати).
• Площу довільного трикутника можна знайти, розділивши твір всіх його сторін на 4 радіуси описаного навколо нього кола (Формула 4).
• Формула 5 являє собою знаходження площі трикутника через довжини його сторін і його напівпериметр (половину суми всіх його сторін).
• Формула Герона (6) - це визначння тієї ж самої формули без використання поняття напівпериметр, тільки через довжини сторін.
• Площа довільного трикутника дорівнює добутку квадрату сторони трикутника на синуси прилеглих до цієї сторони кутів, поділеного на подвійний синус протилежного цій стороні кута (Формула 7).
• Площу довільного трикутника можна знайти як добуток двох квадратів описаного навколо нього кола на синуси кожного з його кутів. (Формула 8).
• Якщо відома довжина одного боку і величини двох прилеглих до нього кутів, то площа трикутника може бути знайдена як квадрат цього боку, поділений на подвійну суму котангенсів цих кутів (Формула 9).
• Якщо відома тільки довжина кожної з висот трикутника (Формула 10), то площа такого трикутника зворотно пропорційна довжині цих висот, як по Формулі Герона. 
• Формула 11 дозволяє обчислити площу трикутника за координатами його вершин, які задані у вигляді значень (x; y) для кожної з вершин. Зверніть увагу, що вийшло значення, яке необхідно взяти по модулю, так як координати окремих (або навіть усіх) вершин можуть перебувати в області негативних значень.
  

Див. також площа рівнобедреного трикутника.

Примітка. Далі наведені приклади розв'язання задач з геометрії на знаходження площі трикутника. Якщо Вам необхідно вирішити задачу з геометрії і схожої на таку тут немає - пишіть про це в форумі. У рішеннях замість символу "квадратний корінь" може застосовуватися функція sqrt (), в якій sqrt - символ квадратного кореня, а в дужках зазначено підкореневий вираз. Іноді для простих підкореневих виразів може використовуватися символ √.

Завдання

Сторони трикутника дорівнюють 5 і 6 см. Кут між ними становить 60 градусів. Знайдіть площу трикутника.

Рішення.

Для вирішення цього завдання використовуємо формулу номер два з теоретичної частини уроку.
Площа трикутника може бути знайдена через довжини двох сторін і синус кута між ними і буде дорівнює
S=1/2 ab sin γ

Оскільки всі необхідні дані для вирішення (відповідно до формули) у нас є, нам залишається тільки підставити значення з умови задачі в формулу:
S = 1/2 * 5 * 6 * sin 60    

У таблиці значень тригонометричних функцій знайдемо і підставами в вираз значення синуса 60 градусiв. Він буде дорівнює кореню з трьох на два.  
S = 15 √3 / 2

Відповідь: 7,5 √3 (в залежності від вимог викладача, ймовірно, можна залишити і 15 √3 / 2)

Завдання

Знайти площу рівностороннього трикутника зі стороною 3 см.

Рішення.

Площа трикутника можна знайти за формулою Герона:

S = 1/4 sqrt( ( a + b + c)(b + c - a)(a + c - b)(a + b -c) )

Оскільки a = b = c формула площі рівностороннього трикутника набуде вигляду:

S = √3 / 4 * a² 

S = √3 / 4 * 3² 

S = 9 √3 / 4

Відповідь: 9 √3 / 4. 

Завдання

У скільки разів збільшиться площа трикутника, якщо сторони збільшити в 4 рази?

Рішення.

Оскільки розміри сторін трикутника нам невідомі, то для вирішення завдання будемо вважати, що довжини сторін відповідно рівні довільним числах a, b, c. Тоді для того, щоб відповісти на питання завдання, знайдемо площу даного трикутника, а потім знайдемо площу трикутника, сторони якого в чотири рази більше. Співвідношення площ цих трикутників і дасть нам відповідь на завдання.

Далі наведемо текстове пояснення рішення задачі по кроках. Однак, в самому кінці, це ж саме рішення приведено в більш зручному для сприйняття графічному вигляді. Бажаючі можуть відразу опуститися в низ рішення.

Для вирішення використовуємо формулу Герона (див. Вище в теоретичній частині уроку). Виглядає вона наступним чином:

S = 1/4 sqrt( ( a + b + c)(b + c - a)(a + c - b)(a + b -c) )  
(див. перший рядок малюнка внизу)

Довжини сторін довільного трикутника задані змінними a, b, c.
Якщо сторони збільшити в 4 рази, то площа нового трикутника з складе:

S₂ = 1/4 sqrt( ( 4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c) ) 
(див. другий рядок на малюнку внизу)

Як видно, 4 - загальний множник, який можна винести за дужки з усіх чотирьох виразів за загальними правилами математики.
тоді

S₂ = 1/4 sqrt( 4 * 4 * 4 * 4 ( a + b + c)(b + c - a)(a + c - b)(a + b -c) ) - на третьому рядку малюнка 
S₂ = 1/4 sqrt( 256 ( a + b + c)(b + c - a)(a + c - b)(a + b -c) ) - четвертий рядок

З числа 256 прекрасно витягується квадратний корінь, тому винесемо його з-під кореня    
S₂ = 16 * 1/4 sqrt( ( a + b + c)(b + c - a)(a + c - b)(a + b -c) ) 
S₂ = 4 sqrt( ( a + b + c)(b + c - a)(a + c - b)(a + b -c) ) 
(див. п'ятий рядок малюнка внизу)

Щоб відповісти на питання, поставлене в завданні, нам достатньо розділити площа отриманого трикутника, на площу початкового.
Визначимо співвідношення площ, розділивши вираження один на одного і скоротивши, вийшла дріб.

S₂ / S = 16 
(див. внизу докладніше запис у вигляді дробу і її скорочення - в останньому рядку)

На малюнку логіка обчислення рішення, описаного вище, наведена вже у вигляді формул (одна за одною)

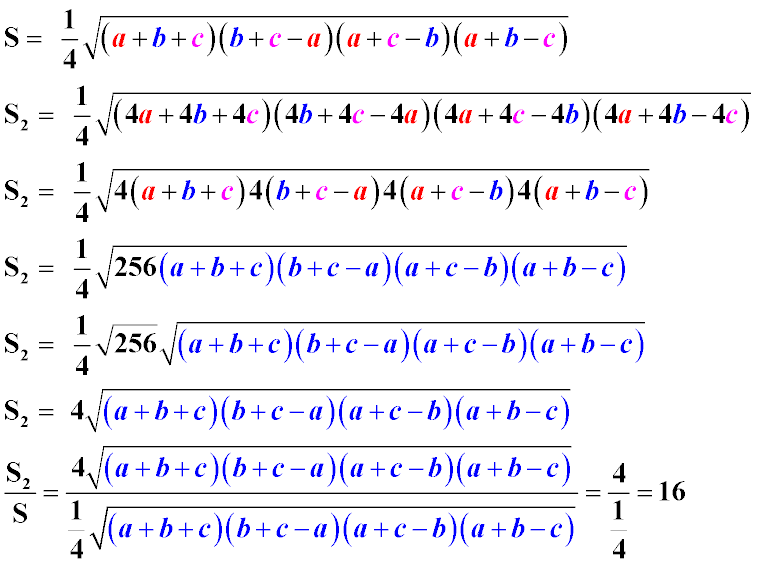
Відповідь: Площа трикутника збільшиться в 16 разів