|
|
Поняття багатокутника. Що таке багатокутник
Багатокутник - це геометрична фігура, що є замкненою ламаною лінією.
Існують декілька варіантів визначення багатокутників:
Багатокутник – це плоска замкнута ламана лінія;
Багатокутник – це плоска замкнута ламана лінія без самоперетинів;
Багатокутник – це частина площини, яка обмежена замкненою ламаною.
Вершини ламаної називаються вершинами багатокутника, а відрізки - сторонами багатокутника.
Вершини багатокутника називаються сусідніми, якщо є кінцями однієї з його сторін.
Відрізки, які з'єднують несусідні вершини багатокутника, називаються діагоналями.
Кутом (або внутрішнім кутом) багатокутника при даній вершині називається кут, утворений його сторонами,
що сходяться в цій вершині, що знаходиться у внутрішній області багатокутника.
Зовнішнім кутом опуклого багатокутника при цій вершині називається кут, суміжний внутрішньому куту
багатокутника при цій вершині. У загальному випадку зовнішній кут це різниця між 180° та внутрішнім кутом
Багатокутник називають опуклим, за умови, що одна з таких умов є вірною:
- Випуклий багатокутник лежить по одну сторону від будь-якої прямої, що з'єднує сусідні вершини;
-
Випуклий багатокутник є перетином декількох напівплощин;
-
Будь-який відрізок з кінцями в точках, що належать опуклому багатокутнику, повністю належить йому.
-
Випуклий багатокутник називається правильним, якщо у нього всі сторони рівні і всі кути рівні, наприклад,
рівносторонній трикутник, квадрат і правильний п'ятикутник.
Випуклий багатокутник називається вписаним у коло, якщо всі його вершини лежать на одному колі.
Випуклий багатокутник називається описаним біля кола, якщо всі його сторони торкаються деякого кола.
Класифікація (види) багатокутників
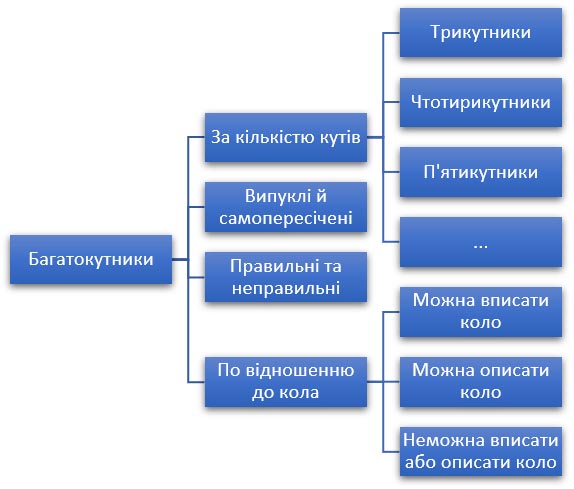
Класифікація багатокутників за видами може бути за багатьма властивостями, найголовніші з них:
- кількість вершин
-
опуклість
-
правильність
-
можливість вписати або описати коло
Багатокутник з трьома вершинами називається трикутником (див. трикутник), багатокутник із чотирма вершинами називається чотирикутник (див. чотирикутник) і так далі за кількістю вершин.
Випуклий багатокутник лежить завжди по одну сторону від прямої, яка містить будь-яку його сторону. (Див. вище)
У правильного багатокутника рівні всі боки та кути. Завдяки цьому вони мають деякі особливі властивості (див. квадрат).
Самопересічні багатокутники також можуть бути правильними. Наприклад, пентаграма ("п'ятикутна зірка").
Також багатокутники можна розрізняти стосовно можливості вписати в багатокутник або описати коло біля багатокутника. Можуть бути багатокутники, навколо яких не можна описати коло, а також вписати його. Разом з тим навколо будь-якого трикутника завжди можна описати коло.
Властивості багатокутника
Сума внутрішніх кутів n-кутника дорівнює (n − 2)π.
Сума внутрішніх кутів правильного n-кутника дорівнює 180(n − 2).
Число діагоналей будь-якого багатокутника дорівнює n(n − 3) / 2, де n – число сторін.
Висота паралелограма |
Описание курса
| Шестикутник
|

