Примітка. Це частина уроку з завданнями по геометрії (розділ теорема синусів). Якщо Вам необхідно вирішити задачу з геометрії, якої тут немає - пишіть про це в форумі. У завданнях замість символу "квадратний корінь" застосовується функція sqrt (), в якій sqrt - символ квадратного кореня, а в дужках зазначено підкоренний вираз.
Теорема синусів:
Сторони трикутника пропорційні синусам протилежних кутів, або, в розширеному формулюванні:
де
R - радіус описаного кола.
Теорію - формулювання і доведення теореми детально див. В розділі "
Теорема синусів".
Завдання. Знайти сторону трикутника
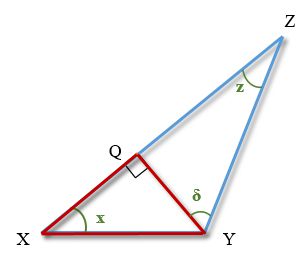
У трикутнику XYZ кут Х = 30 кут Z = 15. Перпендикуляр YQ до ZY ділить сторону ХZ на частини XQ і QZ.
Знайти XY, якщо QZ = 1.5м
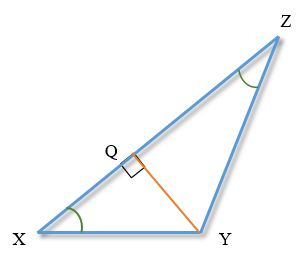Рішення.
Висота утворила два прямокутних трикутника XYQ і ZYQ.
Для вирішення завдання скористаємося теоремою синусів.
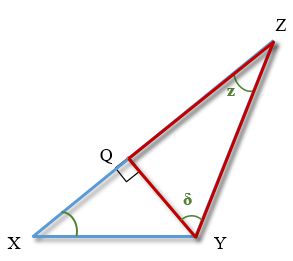
Для трикутника QYZ буде вірним співвідношення:
QZ / sin δ = QY / sin z
Оскільки прямокутник QYZ прямокутний, сума кутів будь-якого трикутника дорівнює 180 градусам, при цьому
z = 15 градусов, то ∠δ = 180 - 90 - 15 = 75
Візьмемо до уваги
табличні значення деяких тригонометричних функцій:
- синус 15 градусів дорівнює sin( 15 ) =
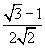
- синус 75 градусів дорівнює sin( 75 ) =
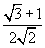
Пояснення до вирішення на зображенні вище.
Записуємо формулювання теореми синусів на прикладі обраного трикутника
Перший рядок:
QZ / sin( 75 ) = QY / sin( 15 )
Другий рядок:
підставимо значення синуса кутів 75 і 15 градусів з таблиці
QZ / ( ( √3 + 1 ) / ( 2√2 ) ) = QY / ( ( √3 - 1 ) / ( 2√2 ) )
Третій рядок - спрощуємо вираз
QZ * 2√2 / ( √3 + 1 ) = QY * 2√2 / ( √3 - 1 )
У четвертому рядку скорочуємо ліву і праву частину на 2√2
QZ / ( √3 + 1 ) = QY / ( √3 - 1 )
П'ятий рядок:
Врахуємо, що довжина QZ нам відома і вказана в умові завдання. Підставами її в вираз
Тепер можна знайти значення висоти QY
QY = 3/2 ( √3 - 1 ) / ( √3 + 1 )
Друга частина рішення.
Оскільки довжина висоти QY трикутника тепер відома, знайдемо величину XY за допомогою теореми синусів.
QY / sin( 30 ) = XY / sin( 90 )
Далі вирішуємо аналогічно першої частини рішення.
Візьмемо до уваги табличні значення деяких тригонометричних функцій:
- синус 30 градусів дорівнює sin( 30 ) = 1 / 2
- синус 90 градусів дорівнює sin( 90 ) = 1
тоді
QY = XY sin ( 30 )
3/2 ( √3 - 1 ) / ( √3 + 1 ) = 1/2 XY
XY = 3 ( √3 - 1 ) / ( √3 + 1 ) ≈ 0.8 м
Відповідь: 0,8 м или 3 ( √3 - 1 ) / ( √3 + 1 )
