Завдання 1.

У правильній трикутній піраміді бічні грані нахилені до основи під кутом 60°.
Відстань від центру основи до бічної грані дорівнює 2√3. 

Знайти об’єм піраміди.

1. Центр правильного трикутника в основі:

У правильній трикутній піраміді центр основи (центр вписаного кола правильного трикутника) збігається з точкою перетину медіан трикутника.

Нехай довжина сторони основи правильного трикутника дорівнює aa. Відстань від центру основи до бічної грані — це радіус кола, вписаного в
трикутник. Він обчислюється за формулою:




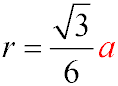
За умовою задачі, ця відстань дорівнює 2√3. Отже:

a√3 / 6=2√3.

Розв’яжемо рівняння:
a = 12.

Таким чином, сторона основи дорівнює a = 12.

2. Висота піраміди (H):

Бічна грань — це рівнобедрений трикутник з основою aa та висотою, проведеною з вершини піраміди.
Висота піраміди H утворює кут 60° з площиною основи.

За тригонометричною залежністю:

h = r⋅tan⁡(60°).

Підставимо r=2√3 та tan⁡(60°)=√3

h = 2√3⋅√3 = 6

Отже, висота піраміди дорівнює h = 6.

3. Площа основи Sосн:

Основа піраміди — правильний трикутник зі стороною a = 12.
Площа правильного трикутника обчислюється за формулою:

.

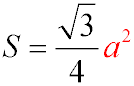Підставимо a = 12:

S = 12² * √3 / 4 = 144 √3 / 4 = 36 √3

4. Об’єм піраміди (V):

Об’єм піраміди визначається за формулою:




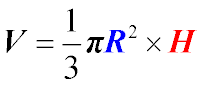
Підставимо Sосн=36√3 та H=6:

V=1 / 3⋅36√3⋅6=72√3

Завдання 2