Прямокутна трапеція

Основні поняття, властивості та формули

Прямокутна трапеція – це трапеція, у якої хоча б один з кутів прямий (класичне визначення).

Примітка: Насправді, у прямокутної трапеції, як мінімум, два прямі кути (див. нижче - властивості).

Інші визначення:

• Прямокутною називається трапеція, у якої одна бічна сторона перпендикулярна основам.
• Трапеція, що має прямі кути при бічній стороні, називається прямокутною.

Формули для прямокутної трапеції

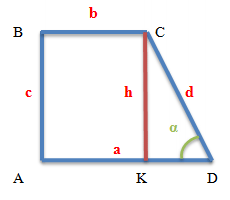
Формули знаходження висоти і бічної грані прямокутної трапеції через основи і гострий кут. Позначення формул дані на кресленні вище.
Відповідно:

• a і b – основи трапеції
• c – бічна сторона прямокутної трапеції, перпендикулярна основам
• d – бічна сторона трапеції, що не є перпендикулярною основам
• α – гострий кут при більшій основі трапеції
• m – середня лінія трапеції

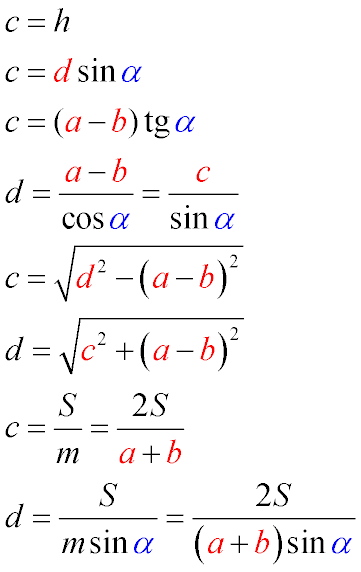
Інтерпретація формул:

1. Бічна сторона прямокутної трапеції, перпендикулярна основам, дорівнює висоті трапеції (Формула 1).
2. Бічна сторона прямокутної трапеції, перпендикулярна основам, дорівнює добутку синуса гострого кута при більшій основі на довжину другої бічної сторони. (Трикутник CKD – прямокутний, відповідно h/d=sin⁡ α згідно з властивостями синуса, а c=h) (Формула 2).
3. Бічна сторона, перпендикулярна основам, дорівнює добутку різниці основ на тангенс гострого кута при більшій основі. (Трикутник CKD – прямокутний. Оскільки трапеція – прямокутна, то довжина KD – це і є різниця основ, а h/KD=tg⁡ α за визначенням тангенса, а c = h, звідки c/KD=tg⁡ α) (Формула 3).
4. Бічна сторона, яка не перпендикулярна основам, дорівнює частці різниці основ до косинуса гострого кута при більшій основі або частці висоти трапеції і синуса гострого кута при більшій основі. (Різниця основ дорівнює KD. У прямокутному трикутнику CKD за визначенням косинуса cos⁡α = KD/d, звідки і випливає шукану формулу) (Формула 4).
5. Бічна сторона прямокутної трапеції, яка не перпендикулярна основам, дорівнює квадратному кореню з різниці квадрата другої бічної сторони і квадрата різниці основ. (Різниця основ дорівнює KD, KC дорівнює другій бічній стороні. Трикутник CKD, далі – наслідок з теореми Піфагора – з квадрата гіпотенузи віднімаємо квадрат катета і витягуємо з отриманого виразу квадратний корінь, знаходимо шуканий катет) (Формула 5).
6. Бічна сторона прямокутної трапеції, перпендикулярна основам, дорівнює квадратному кореню з суми квадрата другої бічної сторони і квадрата різниці основ. (Різниця основ дорівнює KD, KC дорівнює другій бічній стороні. Трикутник CKD, прямокутний, далі – наслідок з теореми Піфагора – знаходимо суму квадратів катетів і витягуємо з отриманого виразу квадратний корінь) (Формула 6).
7. Бічна сторона прямокутної трапеції, перпендикулярна основам, дорівнює частці від ділення подвійної площі трапеції на суму її основ. (Оскільки площа трапеції дорівнює добутку середньої лінії трапеції на висоту (S = mh), а h = c, то розділивши площу на середню лінію прямокутної трапеції, отримаємо її висоту, а підставивши у формулу значення середньої лінії (m = (a + b) / 2), отримаємо шукану формулу) (Формула 7).
8. Бічна сторона прямокутної трапеції, яка не перпендикулярна основам, дорівнює частці від ділення подвійної площі трапеції на добуток суми її основ і синуса гострого кута при основі. (Оскільки площа трапеції дорівнює добутку середньої лінії трапеції на висоту (S = mh), а h = c, то розділивши площу на середню лінію прямокутної трапеції, отримаємо її висоту, а виразивши висоту через другу бічну сторону і підставивши у формулу значення середньої лінії (m = (a + b) / 2), отримаємо шукану формулу) (Формула 8).

Оскільки прямокутна трапеція – це окремий випадок трапеції, то інші формули і властивості можна подивитися в розділі "Трапеція".

Властивості прямокутної трапеції

• У прямокутної трапеції два кути обов'язково прямі.
• Обидва прямі кути прямокутної трапеції обов'язково належать суміжним вершинам.
• Обидва прямі кути в прямокутній трапеції обов'язково прилягають до однієї і тієї ж бічної сторони.
• Діагоналі прямокутної трапеції утворюють з однією з бічних сторін прямокутний трикутник.
• Довжина бічної сторони трапеції, перпендикулярної основам, дорівнює її висоті.
• У прямокутної трапеції основи паралельні, одна бічна сторона перпендикулярна основам, а друга бічна сторона – нахилена до основ.
• У прямокутної трапеції два кути прямі, а два інших – гострий і тупий.

Задача

У прямокутній трапеції більша бічна сторона дорівнює сумі основ, висота дорівнює 12 см.
Знайдіть площу прямокутника, сторони якого дорівнюють основам трапеції.

Розв'язання: Позначимо трапецію як ABCD. Позначимо довжини основ трапеції як a (більша основа AD) і b (менша основа BC).
Нехай прямим кутом буде ∠A.

Площа прямокутника, сторони якого дорівнюють основам трапеції, буде дорівнювати:

З вершини C верхньої основи трапеції BCD опустимо на нижню основу висоту CK.
Висота трапеції відома за умовою задачі. Тоді, за теоремою Піфагора:

Оскільки велика бічна сторона трапеції за умовою дорівнює сумі основ, то CD = a + b

Оскільки трапеція прямокутна, то висота, проведена з верхньої основи трапеції, розбиває нижню основу на два відрізки AD = AK + KD.
Величина першого відрізка дорівнює меншої основі трапеції, так як висота утворила прямокутник ABCK, тобто BC = AK = b, отже,
KD дорівнюватиме різниці довжин основ прямокутної трапеції KD = a - b.

тобто

12² + (a - b)² = (a + b)²
звідкі
144 + a² - 2ab + b² = a² + 2ab + b²
144 = 4ab

Оскільки площа прямокутника S = ab (див. вище), то

144 = 4S
S = 144 / 4 = 36