|
|
Визначення хорди
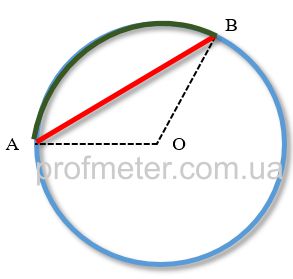
Хорда - це відрізок, який з'єднує дві точки заданої кривої. Хорда може бути у дуги, окружності, еліпса і т.д.
На малюнку хорда позначена як відрізок AB червоного кольору. Обидва його кінці знаходяться на колі.
Частина кривої, укладеної між двома точками хорди, називається дугою.
На малюнку дуга хорди AB позначена зеленим кольором.
Сегмент – це плоска фігура, укладена між дугою і її хордою.
Сегмент на малюнку обмежений червоним відрізком AB з одного боку, і зеленої дугою - з іншого боку.
Хорда, що проходить через центр кола, називається діаметром кола.
Діаметр кола - найдовша хорда окружності.
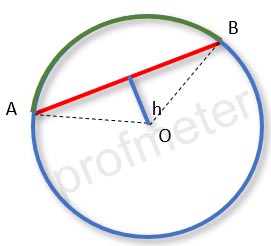
Властивості хорди кола
- Якщо відстані від центру кола до хорд (h) рівні, то ці хорди рівні.
Вірно і зворотне - якщо хорди рівні, то відстані від центру кола до цих хорд (h) рівні.
- Якщо хорда більше, то відстань від центру кола до цієї хорди (h) менше. Якщо хорда менше, то відстань від центру кола до цієї хорди більше.
Вірно і зворотне
- Найбільша можлива хорда є діаметром
- Серединний перпендикуляр до хорди проходить через центр кола
- Якщо діаметр ділить хорду, яка не є діаметром, навпіл, то цей діаметр перпендикулярний цій хорді. Вірно і зворотне - якщо діаметр
перпендикулярний хорді, то цей діаметр ділить цю хорду навпіл
- Якщо діаметр ділить хорду, яка не є діаметром, навпіл, то цей діаметр ділить дуги, що стягнуті цією хордою, навпіл.
Вірно і зворотне - якщо діаметр ділить дугу навпіл, то цей діаметр ділить навпіл хорду, що тисне на цю дугу
- Якщо радіус ділить хорду, яка не є діаметром, навпіл, то цей радіус перпендикулярний цій хорді.
Вірно і зворотне - якщо радіус перпендикулярний хорді, то цей радіус ділить цю хорду навпіл
- Якщо радіус ділить хорду, яка не є діаметром, навпіл, то цей радіус ділить дугу, що стягнута цієї хордою, навпіл.
Вірно і зворотне - якщо радіус ділить дугу навпіл, то цей радіус ділить навпіл хорду, що тисне на цю дугу.
- Якщо радіус перпендикулярний хорді, то цей радіус ділить дугу, що стягнута цією хордою, навпіл.
Вірно і зворотне - якщо радіус ділить дугу навпіл, то цей радіус перпендикулярний хорді, що стягує цю дугу.
![Хорда к окружности вместе с вписанным [1] и центральными углами [2] Хорда к окружности вместе с вписанным [1] и центральными углами [2]](/upload/medialibrary/b1c/horda2.jpg)
Властивості хорди і вписаного кута
На малюнку [1] вписаний кут позначений як ACB, хорда кола – AB
- Якщо вписані кути спираються на одну й ту ж хорду і вершини цих кутів лежать по одну сторону цієї хорди, то ці кути рівні.
- Якщо пара вписаних кутів спирається на одну і ту ж хорду і вершини цих кутів лежать по різні боки цієї хорди, то сума цих кутів дорівнює 180°.
- Якщо вписаний і центральний кути спираються на одну й ту ж хорду і вершини цих кутів лежать по одну сторону цієї хорди, то вписаний кут
дорівнює половині центрального кута.
- Якщо вписаний кут спирається на діаметр, то цей кут є прямим.
Властивості хорди і центрального кута
На малюнку [2] центральний кут позначений як AOB, хорда як AB.
- Если хорды стягивают равные центральные углы, то эти хорды равны.
- Если хорды равны, то эти хорды стягивают равные центральные углы.
- Большая хорда стягивает больший центральный угол, меньшая хорда стягивает меньший центральный угол.
- Больший центральный угол стягивается большей хордой, меньший центральный угол стягивается меньшей хордой.
Формули знаходження хорди
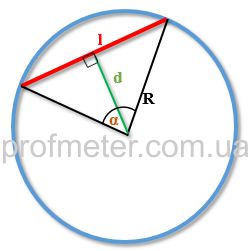
Позначення в формулах:
l - довжина хорди
α - величина центрального кута
R - радіус кола
d - довжина перпендикуляра, проведеного від центру кола до хорди
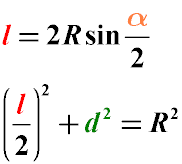
Довжина хорди окружності (l) дорівнює подвоєному радіусу даної окружності (R), помноженому на синус половини центрального кута.
Сума квадрата половини довжини хорди і квадрата перпендикуляра, проведеного до цієї хорді, дорівнює квадрату радіусу кола.
Дана формула випливає з теореми Піфагора.
Вирішення завдань
Примітка. Якщо Ви не знайшли рішення відповідної задачі, пишіть про це в форумі. Напевно, курс геометрії буде доповнений.
Завдання.
Хорди АВ і СD перетинаються в точці S, при чому AS: SB = 2: 3, DS = 12см, SC = 5 см, знайти АВ.
Рішення.

Оскільки співвідношення AS: SB = 2: 3, то нехай довжина AS = 2x, SB = 3x
Відповідно до властивості хорд AS x SB = CS x SD, тоді
2х * 3х = 5 * 12
6х2 = 60
х2 = 10
x = √10
Звідки
AB = AS + SB
AB = 2√10 + 3√10= 5√10
Відповідь: 5√10
Завдання.
Окружність розділена на частини, які відносяться як 3,5: 5,5: 3 і точки поділу з'єднані між собою. Визначити величину кутів утвореного трикутника.
Рішення.
Позначимо коефіцієнт пропорційності дуг окружності, як х. З'єднаємо центри окружності з кінцями дуг. Оскільки центральний кут дорівнює
градусній мірі дуги, на яку спирається, то співвідношення центральних кутів кола дорівнюватиме співвідношенню її частин (дуг).
Оскільки градусна міра кола дорівнює 360 градусам, то
3,5х + 5,5х + 3х = 360
12х = 360
х = 30
Звідки градусні величини центральних кутів рівні:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165
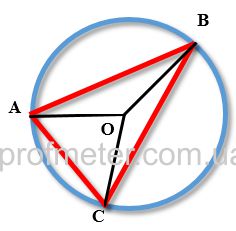
Кути утвореного трикутника є кутами, вписаними в коло. Вписаний кут дорівнює половині градусної міри дуги, на яку спирається.
Звідки кути трикутника рівні:
90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5
Відповідь: Величина кутів трикутника дорівнює 45 ; 52,5 ; 82,5 ;
Коло. Рiвняння кола |
Описание курса
| Еліпс
|

