Геометричне місце точок. Метод геометричних місць
Визначення: Геометричним місцем точок називається геометрична фігура на площині, кожна точка якої володіє однією і тією же певною властивістю.
Метод геометричних місць застосовується найчастіше при побудовах. Наприклад, серединний перпендикуляр до відрізка можна визначити як геометричне місце точок, рівновіддалених від точок кінців відрізків; окружність можна визначити як геометричне місце точок, рівновіддалених від даної точки.
Теорема (про геометричне місце точок). Геометричне місце точок, рівновіддалених від двох даних точок, є пряма, перпендикулярна відрізку, що з'єднує ці точки, і проходить через його середину.
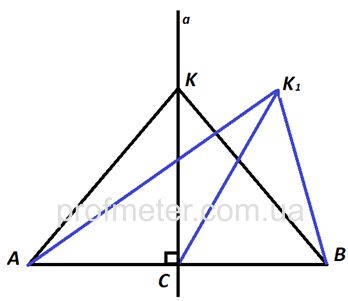
Доведення. Нехай дано точки А і В, а точка С
- середина відрізка АВ. Потрібно знайти геометричне місце точок, рівновіддалених від точок А і В.
Доказ заснований на властивості серединного перпендикуляра до відрізка.
Серединний перпендикуляр СК, що належить прямій а, як і будь-яка точка цієї прямої, - є геометричне місце точок, рівновіддалених від А
і В, так як СКꓕАВ.
Припустимо, що є ще точка К1, відстань до якої від А
і В
однаково.
Розглянемо ΔАК1В, він розбитий відрізком К1С на два трикутника: ΔАК1С і ΔК1СВ. Якщо ці трикутники рівні, то точка К1 теж знаходиться на однаковій відстані від А
і В.
Через точку С проходять дві прямі СК і СК1. На підставі теореми 16 (про єдиність перпендикуляра з точки до прямої), якщо СКꓕАВ з побудови, то СК1
не може бути перпендикулярна АВ.
Так як з двох суміжних кутів (∟К1СА і ∟К1СВ) один повинен бути гострий, а другий - тупий, то ΔК1СА≠ΔК1СВ, отже, К1А≠К1В (є дві рівні сторони, АС=ВС
і К1С- спільна, але немає рівних кутів між ними), значить, К1С - похила до АВ
і АК1
≠ ВК1.
Метод геометричних місць
Визначення: Суть методу геометричних місць в тому, що при наявності не одного, а декількох умов для побудови геометричної фігури, потрібно побудувати кілька геометричних фігур, які по черзі будуть задовольняти кожній з умов, а потім знайти таке геометричне місце точок, яке при перетинанні або поєднанні цих фігур буде відповідати всім умовам побудови.
Наприклад: Дано три точки: А, В, С.
Побудувати точку Х, рівновіддаленість від А і В і знаходиться на відстані h від точки С.
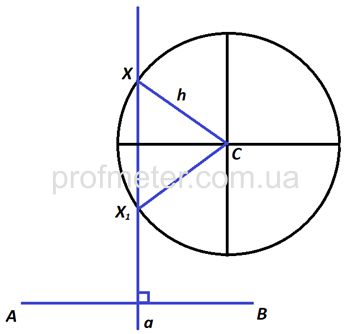
Порядок побудови:
1.Будуємо геометричне місце точок, що задовольняє першій умові: це буде серединний перпендикуляр до відрізка АВ. Пряма а, яка містить серединний перпендикуляр до відрізка АВ, задовольняє повністю першій умові.
2.На перпендикулярі (пряма а) повинна знаходитись точка Х, яка задовольняла б другій умові (відстань від неї до С має становити h).
Якщо з точки С радіусом h провести окружність, то всі крапки окружності будуть розташовані від С на однаковій відстані h
(побудоване друге геометричне місце точок, рівновіддалених від С).
3.Перетин першого геометричного місця точок (пряма а) і другого (окружності з центром в точці С) буде задовольняти обом умовам задачі. Точки перетину кола і прямої (Х1 і Х) і будуть тими шуканими точками, які рівновіддалені від точок А
і В
і знаходяться від С на відстані h.
Точки, відрізки і прямі |
Описание курса
| Центральна і осьова симетрія
|

