|
|
Тригонометричне коло
Тригонометричне коло - це коло з одиничним радіусом і центром на початку осей координат, кожна точка якого утворює трикутник з точками:
- точка на початку осей координат (точка 0; 0)
-
точка на окружності (обрана нами)
-
точка на осі X, яка є проекцією обраної нами точки на цю вісь (перпендикуляр до осі X)
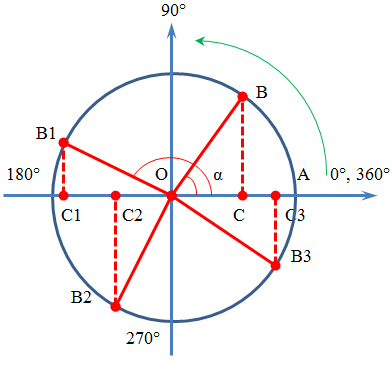
Як видно, такий трикутник є прямокутним, так як з обраної нами точки на вісь абсцис завжди опускається перпендикуляр. Тобто сторона, що з'єднує
початок координат і обрану нами точку на тригонометричному колі (на наведеному малюнку позначену як B, B1. B2, B3) завжди є гіпотенузою
прямокутного трикутника, проекція обраної точки - це катет, а сторона від точки перетину з віссю X утворює другий катет.
Кут, який утворюється між віссю абсцис (віссю X) і гіпотенузою трикутника - є кутом, для якого і обчислюються значення тригонометричних функцій.
Цей кут відраховується від позитивного напрямку осі абсцис (осі X) як нуль, далі проти годинникової стрілки. Таким чином, повне коло становить
360 градусів або 2π радіан.
Щоб обчислити значення тригонометричної функції для вибраного кута тригонометричного кола досить скористатися координатами точки, що
належить колу тригонометричного кола. На наведеному вище малюнку, показано обчислення значення синуса для всіх кутів.
Наприклад, sin α для трикутника OBC (де координати точки B рівні (x, y)), буде дорівнювати:
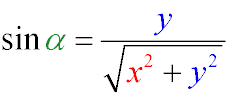
Властивості тригонометричного кола
Якщо послідовно обчислювати значення тригонометричних функцій для тригонометричного кола, то стає видно, що результат таких обчислень
змінює свій знак в залежності від того, в якій чверті тригонометричного кола обрана точка. При цьому знак тригонометричної функції в межах однієї
і тієї ж чверті зберігається.
Знаки тригонометричних функцій в координатних чвертях в тригонометричному колі
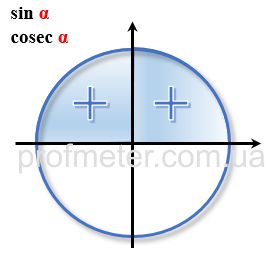
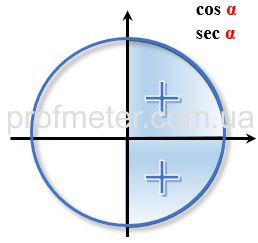
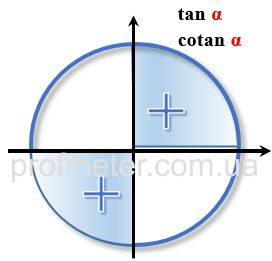
Перетворення кутів більше 360 градусів або 2π радіан
Як видно з картинок, після того, як значення кута перевищить 360 градусів (або 2π радіан), то результат обчислення значення буде тим же самим.
Тобто, для того, щоб привести значення до "нормального" - потрібно відняти від наявного значення 360 градусів або 2π радіан і повторювати
операцію стільки разів, поки результат не стане менше 360 або 2π.
Тангенс та його властивості |
Описание курса
| Таблиця значень тригонометричних функцій
|

