Слово «медіана» перекладається як «рівноподіляюча сторону». Щоб побудувати медіану, треба середину сторони трикутника з'єднати відрізком з протилежною вершиною трикутника. Отриманий відрізок і є медіана трикутника.

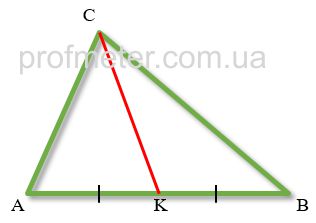
Медіана трикутника - відрізок, проведений з вершини трикутника, що з'єднує цю вершину з серединою протилежної сторони трикутника.

На малюнку червоним кольором позначена медіана CK. При цьому вона ділить сторону AB трикутника навпіл, AK = KB.

Властивості медіани

Всі медіани трикутника перетинаються в одній точці, розташованій в площині трикутника і що є його центром ваги.



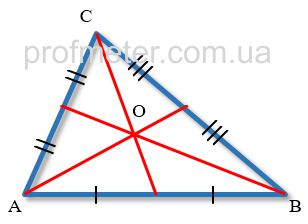
Для визначення цієї точки досить побудувати дві медіани трикутника, і точка їх перетину належатиме третьої медіані цього трикутника.

• Точкою перетину медіан трикутника кожна медіана ділиться у відношенні 2:1, рахуючи від вершини трикутника. Тобто довжина відрізка медіани від вершини трикутника до точки перетину медіан становить 2/3 всієї її довжини, а від точки перетину медіан до сторони трикутника - 1/3 її довжини.
• Медіана розбиває трикутник на два рівновеликих (по площі) трикутника.
• Трикутник ділиться трьома медианами на шість рівновеликих трикутників.
• З сегментів, які формують медіани, можна скласти трикутник, площа якого буде дорівнює 3/4 від всього трикутника. Довжини медіан задовольняють нерівності трикутника.
• У прямокутному трикутнику медіана, проведена з вершини з прямим кутом, дорівнює половині гіпотенузи.
• Більшій стороні трикутника відповідає менша медіана.
• У рівнобедреного трикутника медіана, бісектриса і висота, проведені до основи трикутника, збігаються.
• У рівностороннього трикутника всі три «помітні» лінії (висота, бісектриса і медіана) збігаються і три «помітні» точки (точки ортоцентра, центру ваги і центру вписаного і описаного кіл) знаходяться в одній точці перетину «помітних» ліній, тобто теж збігаються.

Середня лінія трикутника

Відрізок, проведений через основи двох будь-яких медіан трикутника, є його середньою лінією.

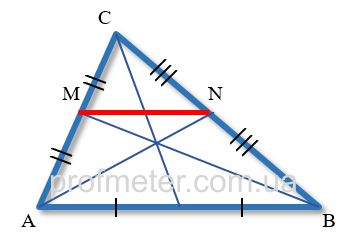
Середня лінія трикутника з'єднує дві точки решт медіан, що лежать на сторонах трикутника

Середня лінія трикутника завжди паралельна тій стороні трикутника, з якої вона не має спільних точок.
Середня лінія трикутника дорівнює половині довжини того боку трикутника, якої вона паралельна.