Призма

Даний розділ присвячений рішенню задач про призми. Для успішного освоєння даного розділу слід взяти до уваги наступне.

Визначення призми

Призма - це об'ємний багатогранник, дві грані якого являють собою рівні (однакові) багатокутники, що лежать у паралельних площинах, а інші грані являють собою паралелограми, протилежнi межі у яких є cпiльними з відповідними сторонами цих паралельних багатокутників.

Нижче, на рисунку зображені трикутна, чотирикутна і похила чотирикутна призма з необхiдними позначеннями. Зазвичай (але не обов'язково) для спрощення розуміння взаємного розташування підстав і їх сторін, позначення нижньої основи починають латинськими літерами А, B, C і так далі, а відповідні сторони верхнього підстави позначають тими ж літерами з додаванням одиниці - А1, B1, C1 і так далі.

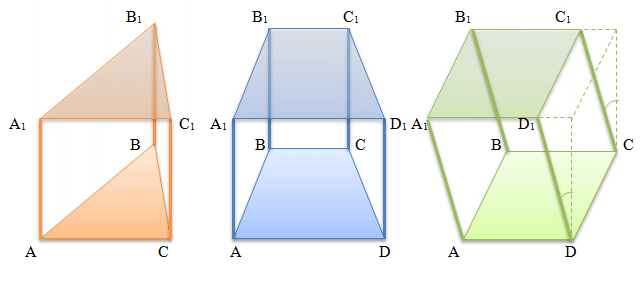
Інші визначення призми:

Призма - багатогранник, основаннями якого є рівні багатокутники, та відповідні бічні грані якого являють собою паралелограми.

Інші визначення:

Рівні багатокутники, що лежать у паралельних площинах, називаються основами призми.

Грані призми, що з'єднують її основи призми (ABCD і A1B1C1D1), називаються бічними гранями. 

Площа (об'єднання, сукупність) всіх бічних граней призми називається бічною поверхнею. 

Загальні межі паралелограмів, що з'єднують основи призми, називаються бічними ребрами. (AA1 BB1 CC1 і т. д.)

Довжина відрізка, що з'єднує основи призми і перпендикулярного одночасно обом основам, називається висотою призми.

Відрізок проведений між двома вершинами багатогранника, що представляє собою призму, так, щоб він не належав ні одній площині призми (основам або бічним граням) називається діагоналлю призми. (АС1)

Площина, що проходить через бічне ребро призми і діагональ основи (не плутати з діагоналлю призми!) називається діагональною площиною. (AA1C1C)

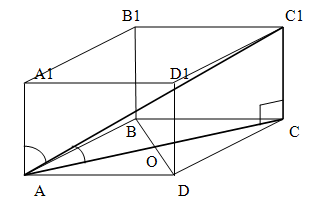
Властивості призми

• Основання призми дорівнюють одне одному
• Кожна з бічних граней обов'язково є паралелограмом
• Бічні ребра призми паралельні і рівні між собою
• Бічні грані призми являють собою рівні прямокутники
• При перетині призми і діагональної площині переріз являє собою паралелограм
• Перпендикулярний переріз перпендикулярно до всіх бічних ребер призми
• Кути перпендикулярного перетину — це лінійні кути двогранних кутів при відповідних бічних ребрах
• Перпендикулярний переріз перпендикулярний до всіх бічних граней

Спеціальні випадки призм

Паралелепіпед - це призма, основанням якої є паралелограм 

Прямокутний паралелепіпед - пряма призма, основою якої є прямокутник і всі межі є прямокутниками

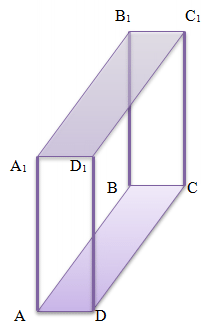
Пряма призма - призма, у якої бічні ребра перпендикулярні площини основи

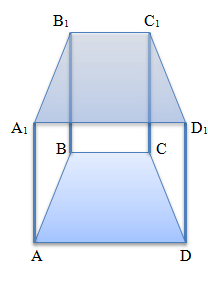
Правильна призма - це пряма призма, основами якої є правильний багатокутник. (див. також - правильна чотирикутна призма)

Куб - це правильна призма, всі сторони якого являють собою правильний чотирикутник (квадрат)

Об'єм призми

Формула знаходження об'єму призми виглядає наступним чином:

V = Sh, де

V - об'єм призми 

S - площа основи призми 

h - висота призми

Площа повної поверхні призми дорівнює сумі площі його бічної поверхні і подвоєною площі основи.

Площа бічної поверхні довільної призми S=P х l, де P — периметр перпендикулярного перерізу, l — довжина бічного ребра.

Площа бічної поверхні прямої призми S=P х h, де P — периметр основи призми, h — висота призми.