Примітка: див. також таблицю значень тригонометричних функцій інших кутів.
Синус, косинус, тангенс кута 45 градусів (sin 45, cos 45, tg 45)
Табличні значення синуса 45, косинуса 45 і тангенса 45 градусів вказані нижче. Далі по тексту йде пояснення методу і правильності
обчислення цих значень для довільного прямокутного трикутника. Ми обчислимо, чому дорівнює синус 45, косинус 45 та тангенс 45.
45 градусів - це π/4 радіан. Формули для значень косинуса, синуса і тангенса пі/4 радіан вказані нижче (хоча вони і тотожні).
Тобто, наприклад, tg π/4 = tg 45 градусів
ЗНАЧЕННЯ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ ПРИ α=45°
Як самостійно обчислити значення sin cos tg 45 градусів?
Створимо i розглянемо прямокутний трикутник АВС в якого кут ∠ В = 45°. На підставі співвідношення його сторін, обчислимо значення
тригонометричних функцій в прямокутному трикутнику для кута 45 градусів. Оскільки трикутник прямокутний, то значення функцій синуса,
косинуса і тангенса дорівнюватимуть співвідношенню його вiдповiдних сторін.
Оскільки значення функцій синуса, косинуса і тангенса залежать виключно від градусної міри кута (або значення, вираженого в радіанах),
то знайдені нами співвідношення і будуть значеннями функції синуса 45, косинуса 45 і тангенса 45 градусів.
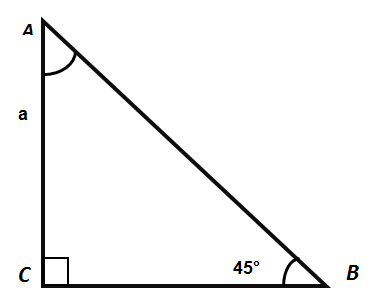
Згідно властивостям прямокутного трикутника, кут С - прямій і дорівнює 90 градусам. Кут B ми спочатку побудували з градусною мірою 45 градусів.
Знайдемо значення кута А. Так як сума кутів трикутника дорівнює 180 градусам, то
∠А + ∠В + ∠С = 180°
Кут C прямiй та дорівнює 90 градусам, кут B ми спочатку визначили як 45 градусів, таким чином:
∠А = 180° -∠С - ∠В = 180° - 90° - 45° = 45°,
Оскільки в даного трикутника два кути рівні між собою, то трикутник АВС – прямокутний, і, одночасно, рівнобедрений, в якому обидва катети рівні
між собою: AC = BC.
Допустимо, що довжина сторін дорiвнює деякому числу АС = ВС = а. Знаючи довжини катетів, обчислимо довжину гіпотенузи.
Згідно теореми Піфагора: АВ2=АС2+ВС2
Замінимо довжини AC і BC на змінну а, тоді отримаємо:
АВ2 = а2 + а2 = 2а2,
тоді АВ=а√2.
В результаті ми виразили довжини всіх сторін прямокутного трикутника з кутом 45 градусів через змінну а.
Згідно властивостей тригонометричних функцій в прямокутному трикутнику співвідношення відповідних сторін трикутника буде рівним
значенню відповідних функцій. Таким чином для кута α = 45 градусів:
sin α = BC / AB (згідно з визначенням синуса для прямокутного трикутника - це відношення катета, що протилежить куту, до гіпотенузи,
BC - катет, AB - гіпотенуза)
cos α = AC / AB (згідно з визначенням косинуса - це відношення прилеглого катета до гіпотенузи, AC - катет, AB - гіпотенуза)
tg α = BC / AC (аналогічно, тангенс для кута α дорівнюватиме відношенню катета, що протилежить, до прилеглого)
Замість позначень сторін підставимо значення їх довжин через змінну а.
Виходячи з цього (див. таблицю значень sin 45, cos 45, tg 45) отримуємо:
Табличні значення sin 45, cos 45, tg 45 (тобто значення синуса 45, косинуса 45 і тангенса 45 градусів можна обчислити як співвідношення
відповідних сторін даного трикутника), підставимо обчислені вище значення довжин сторін в формули і отримаємо результат на зображенні нижче.
Табличні значення: синус 45, косинус 45 і тангенс 45 градусів
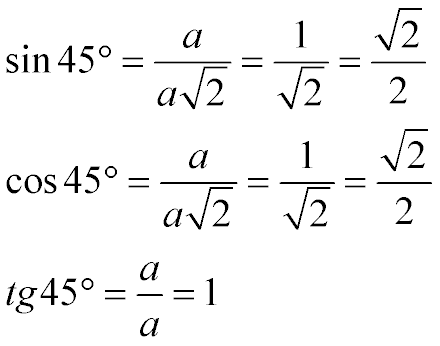
Таким чином:
- тангенс 45 градусів дорівнює одиниці
- синус 45 градусів дорівнює косинусу 45 градусів і дорівнює кореню з двох навпіл (те ж саме, що і одиниця, що ділиться на корінь з двох)
Як видно з обчислень, приведених вище, для обчислення значень відповідної тригонометричної функції важливі не довжини сторін трикутника,
а їх співвідношення, яке завжди одне і те ж для однакових кутів, незалежно від розмірів конкретного трикутника.
Синус, косинус і тангенс кута π/4 радіан
У завданнях, пропонованих для вирішення в старших класах і на ЗНО/ЕГЭ замість градусної міри кута часто зустрічається вказівка
на його величину, виміряну в радіанах. Міра кута, виражена в радіанах, базується на числі пі, яке виражає залежність довжини окружності до її діаметра.
Для простоти розуміння, рекомендую запам'ятати простий принцип перекладу градусів в радіани. Діаметр окружності охоплює дугу,
яка дорівнює 180 градусам. Таким чином, пі радіан буде дорівнює 180 градусам. Звідки легко перерахувати будь-яку градусну міру кута в радіани і назад.
Врахуємо, що кут 45 градусів, виражений в радіанах, дорiвнює (180 / 45 = 4) π/4 ( пі на чотири). Тому знайдені нами значення вірні
для тієї ж самої градусної міри кута, вираженої в радіанах:
- тангенс π/4 ( пі на чотири) дорівнює одиниці
- синус π/4 ( пі на чотири) градусів дорівнює косинусу π/4 градусів і дорівнює корню з двох навпіл
Для зручності зорового сприйняття ці значення наведені на малюнку нижче.
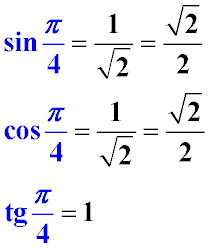
Примітка: див. також таблицю значень тригонометричних функцій інших кутів.

