Циліндр
ВИЗНАЧЕННЯ ЦИЛІНДРА ТА ЙОГО ЕЛЕМЕНТІВ
Циліндр (круговий циліндр) - тіло, яке складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів.
Круги називаються основами циліндра, а відрізки, що сполучають відповідні точки кіл кругів, - твірні циліндра. Ці відрізки утворюють циліндричну поверхню, що є бічною поверхнею циліндра.
Якщо основами циліндра не є кола, то циліндр може бути еліптичним. Зазвичай, такі види циліндра в елементарній геометрії не розглядаються.
Альтернативне визначення.
Циліндром називається геометричне тіло, обмежене циліндричною поверхнею і двома перетинаючими її паралельними площинами.
Повна поверхня циліндра складається з основ і бічної поверхні.
Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ.
Прямий циліндр наочно можна представити як тіло, отримане в результаті обертання прямокутника навколо сторони як осі.
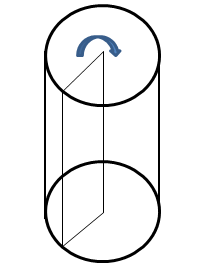
Радіусом циліндра називається радіус його основи.
Висотою циліндра називається відстань між площинами його основ.
Віссю циліндра називається пряма, що проходить через центри основ. Вона паралельна утворюючим.
Переріз циліндра площиною, паралельною до його осі, являє собою прямокутник. Дві сторони його - твірні циліндра, а дві інші - паралельні хорди підстав. Осьовий переріз циліндра - це переріз площиною, яка проходить через його вісь.
Дотичною площиною до циліндра називається площина, що проходить через твірну циліндра і перпендикулярна до площини осьового перерізу, що містить цю твірну.
Об'єм циліндра
Об'єм циліндра дорівнює добутку площі основи на висоту Н [1]:
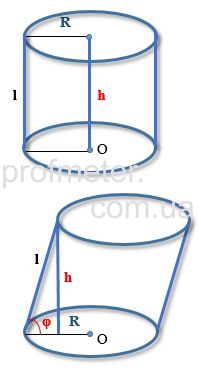
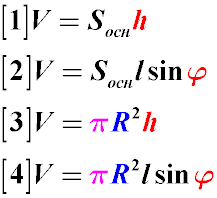
Якщо у циліндра відомі тільки площа основи і утворює, то обсяг такого циліндра буде дорівнює добутку площі основи на утворюючу і синус кута між основою і утворюючої [2].
Для циліндра, в основі якого лежить коло, об'єм циліндра буде дорівнювати площі кола на висоту [3] [4]
Площа бічної поверхні циліндра
Площа бічної поверхні циліндра з радіусом R основи і висотою Н
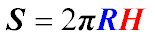
Начать курс обучения
|

