|
Примечание. В данном уроке изложены теоретические материалы и решение задач по геометрии на тему "медиана в прямоугольном треугольнике". Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. Почти наверняка курс будет дополнен.
Свойства медианы прямоугольного треугольника
Определение медианы
|
Медианой треугольника называется отрезок, соединяющий один из углов треугольника с серединой противолежащей ему стороны.
(медианой также называют прямую, содержащую данный отрезок)
|
- Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины угла. Точка их пересечения называется центром тяжести треугольника (относительно редко в задачах для обозначения этой точки используется термин "центроид"),
- Медиана разбивает треугольник на два равновеликих треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников.
- Большей стороне треугольника соответствует меньшая медиана.
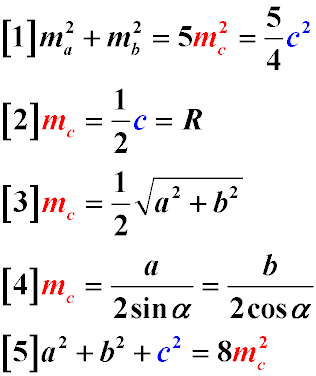
Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.
- Сумма квадратов медиан, опущенных на катеты прямоугольного треугольника равна пяти квадратам медианы, опущенной на гипотенузу (Формула 1)
- Медиана, опущенная на гипотенузу прямоугольного треугольника равна половине гипотенузы (Формула 2)
- Медиана, опущенная на гипотенузу прямоугольного треугольника, равна радиусу окружности, описанной вокруг данного прямоугольного треугольника (Формула 2)
- Медиана, опущенная на гипотенузу, равна половине корня квадратного из суммы квадратов катетов (Формула 3)
- Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два синуса противолежащего катету острого угла (Формула 4)
- Медиана, опущенная на гипотенузу, равна частному от деления длины катета на два косинуса прилежащего катету острого угла (Формула 4)
- Сумма квадратов сторон прямоугольного треугольника равна восьми квадратам медианы, опущенной на его гипотенузу (Формула 5)
Обозначения в формулах:
a, b - катеты прямоугольного треугольника
c - гипотенуза прямоугольного треугольника
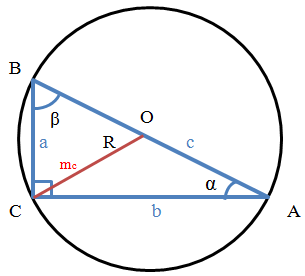
Если обозначить треугольник, как ABC, то
ВС = а
AC = b
AB = c
(то есть стороны a,b,c - являются противолежащими соответствующим углам)
ma - медиана, проведенная к катету а
mb - медиана, проведенная к катету b
mc - медиана прямоугольного треугольника, проведенная к гипотенузе с
α (альфа) - угол CAB, противолежащий стороне а
Задача про медиану в прямоугольном треугольнике
Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно, 3 см и 4 см. Найдите гипотенузу треугольника
Решение
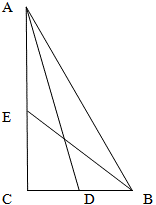
Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике. В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y).
Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC - общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора
AC2 + CD2 = AD2
Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4x2 + y2 = 9
Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
По теореме Пифагора:
EC2 + BC2 = BE2
Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x2 + 4y2 = 16
Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений.
4x2 + y2 = 9
x2 + 4y2 = 16
Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5x2 + 5y2 = 25
5( x2 + y2 ) = 25
x2 + y2 = 5
Обратимся к исходному треугольнику ABC. По теореме Пифагора
AC2 + BC2 = AB2
Так как длина каждого из катетов нам "известна", мы приняли, что их длина равна 2x и 2y, то есть
4x2 + 4y2 = AB2
Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки
4 ( x2 + y2 ) = AB2
Чему равно x2 + y2 мы уже знаем (см. выше x2 + y2 = 5), поэтому просто подставим значения вместо x2 + y2
AB2 = 4 х 5
AB2 = 20
AB = √20 = 2√5
Ответ: длина гипотенузы равна 2√5
Угол между высотой и медианой треугольника |
Описание курса
| Подобие треугольников
|

