У цьому уроці приведені визначення і властивості правильної трикутної піраміди і її окремого випадку - тетраедра (див. Нижче). Посилання на приклади розв'язання задач наведені в кінці уроку.
Визначення
Правильна трикутна піраміда - це піраміда, основою якої є правильний трикутник, а вершина проектується в центр основи.
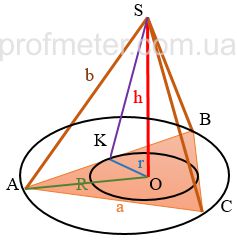
На малюнку позначені:
ABC - Основа піраміди
OS - Висота
KS - Апофема
OK - радіус кола, вписаного в основу
AO - радіус кола, описаного навколо основи правильної трикутної піраміди
SKO - двогранний кут між основою і гранню піраміди (в правильній піраміді вони рівні)
Важливо. У правильній трикутній піраміді довжина ребра (на малюнку AS, BS, CS) може не дорівнювати довжині сторони основи (на малюнку AB, AC, BC). Якщо довжина ребра правильної трикутної піраміди дорівнює довжині сторони основи, то така піраміда називається тетраедром (див. Нижче).
Властивості правильної трикутної піраміди:
- бічні ребра правильної піраміди рівні
- всі бічні грані правильної піраміди є рівнобiчними трикутниками
- в правильну трикутну піраміду можна як вписати, так і описати навколо неї сферу
- якщо центри вписаного і описаного навколо правильної трикутної піраміди, сфери збігаються, то сума плоских кутів при вершині піраміди дорівнює π (180 градусів), а кожен з них відповідно дорівнює π / 3 (пі ділити на 3 або 60 градусів)
- площа бічної поверхні правильної піраміди дорівнює половині добутку периметра основи на апофему
- вершина піраміди проектується на основу в центр правильного рівностороннього трикутника,, який є центром вписаного кола і точкою перетину медіан
Формули для правильної трикутної піраміди
Формула об'єму правильної трикутної піраміди:
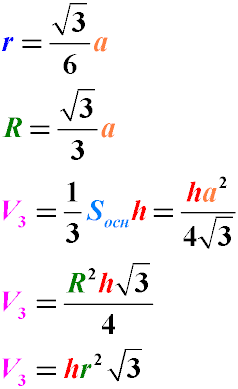
де
V - об'єм правильної піраміди, що має в основі правильний (рівносторонній) трикутник
h - висота піраміди
a - довжина сторони основи піраміди
R - радіус описаного кола
r - радіус вписаного кола
Оскільки правильна трикутна піраміда є окремим випадком правильної піраміди, то формули, які вірні для правильної піраміди, вірні і для правильної трикутної - див. формули для правильної піраміди.
Приклади розв'язання задач:
Тетраедр
Окремим випадком правильної трикутної піраміди є тетраедр.
Тетраедр - це правильний багатогранник (правильна трикутна піраміда) у якій всі грані є правильними трикутниками.
У тетраедра:
-
Всі грані рівні
-
4 грані, 4 вершини і 6 ребер
-
Всі двогранні кути при ребрах і все тригранні кути при вершинах рівні
Медіана тетраедра - це відрізок, що з'єднує вершину з точкою перетину медіан протилежної грані (медіан рівностороннього трикутника, протилежного вершині)
Бімедіана тетраедра - це відрізок, що з'єднує середини перехресних ребер (з'єднує середини сторін трикутника, що є однією з граней тетраедра)
Висота тетраедра - це відрізок, що з'єднує вершину з точкою протилежної грані і перпендикулярний цій межі (тобто є висотою, проведеної від будь-якої грані, також збігається з центром описаного кола).
Тетраедр має такі властивості:
-
Всі медіани і бімедіани тетраедра перетинаються в одній точці
-
Ця точка ділить медіани у відношенні 3: 1, рахуючи від вершини
-
Ця точка ділить бімедіани навпіл
Площа, обсяг, висота, радіус вписаного і описаного кола і інші формули для тетраедра
Див. приклади розв'язання задач: формули і властивості тетраедра.
