|
см. также синус некоторых углов (sin 60, sin 30, sin 45).
Синус угла

Для прямоугольного треугольника ABC синусом (sin) угла A будет соотношение сторон BC и AB.
Синус угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
sin A = BC / AB
Значение функции синуса угла альфа в прямоугольном треугольнике будет всегда одинаковым для одного и того же угла независимо от размеров сторон треугольника.
Функция синус угла (sin)
СИНУС (sin) – тригонометрическая величина, функция угла, изменяющаяся с изменением угла. «Синус» переводится с латинского как «изгиб», «кривизна».
Двигая подвижный радиус по полному кругу против часовой стрелки, получаем положительные углы от 0° до 360°.
Двигая подвижный радиус по полному кругу по часовой стрелке, получаются отрицательные углы, соответственно от 0° до -360°.
В прямоугольном треугольнике сторона, противолежащая прямому углу, называется гипотенузой, а остальные стороны – катетами.
Синус острого угла в прямоугольном треугольнике есть отношение противолежащего катета к гипотенузе.
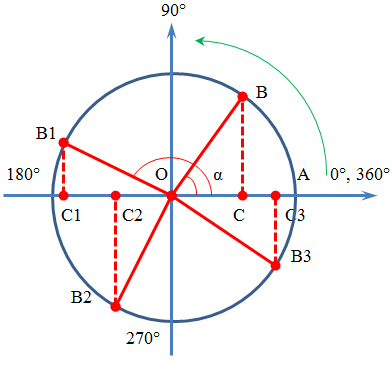
Рассмотрим на окружности изменения функции синуса острого угла, построив на неподвижной стороне угла (ОА) катет прямоугольного треугольника (ОС), у которого гипотенузой будет подвижный радиус (ОВ) (Рис. 1).
По определению синуса угла: sin a=ВС / ОВ .
Для единичной окружности, где ОВ = 1, это длина отрезка ВС. Следовательно, синус угла – это величина проекции подвижного отрезка ОВ на ось у.
Рассмотрим изменения функции sin α (отрезка ВС) при движении подвижного радиуса по окружности и увеличении угла. Пределы изменения синуса угла будем определять по квадрантам.
В I квадранте ( ВС ):
при α = 0º sin α = 0;
при 0º < α < 90º 0 < sin α < 1;
при α = 90º sin α = 1.
Во II квадранте ( В1С1 ):
при α = 90º sin α = 1;
при 90º < α < 180º 1 > sin α > 0;
при α = 180º sin α = 0.
За пройденный первый полукруг sin α изменился от 0 до 0, а наибольшее его значение, равное 1, совпадает с длиной радиуса на положительной полуоси у.
Второй полукруг движения подвижного радиуса можно рассматривать как положительное направление (при движении ОВ дальше против часовой стрелки) и как отрицательное направление (если ОВ вращать по часовой стрелке). Рассмотрим только положительное направление.
В III квадранте ( В2С2 ):
при α = 180º sin α = 0;
при 180º < α < 270º 0 > sin α > -1;
при α = 270º sin α = -1;
В IV квадранте ( В3С3 ):
при α = 270º sin α = -1;
при 270º < α < 360º -1 < sin α < 0;
при α = 360º sin α = 0.
За пройденный второй полукруг sin α изменился от 0 до 0, а наименьшее его значение, равное -1, совпадает с длиной радиуса, но отрицательной полуоси у.
За весь оборот подвижного радиуса ОВ, от совпадения с ОА до второго их совпадения, угол численно изменился от 0º до 360º, а численное значение синуса угла изменялось в пределах от 1 до -1.
см. также - таблица значений основных углов тригонометрических функций.
Начать курс обучения
|

