|
|
Прямая призма
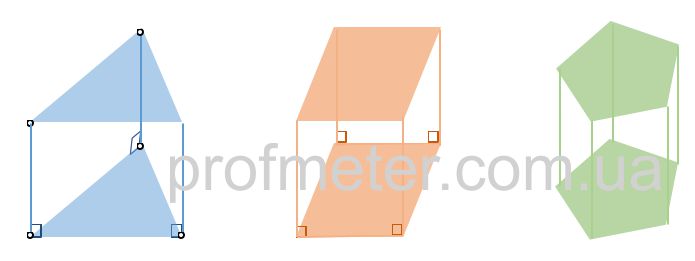
Прямая призма - призма, у которой боковые ребра перпендикулярны плоскости основания.
При этом в основании прямой призмы может быть любая геометрическая фигура.
Правильная прямая призма - это призма, в основаниях которой лежит правильный многоугольник.
Например, правильная прямая четырехугольная призма - это параллелепипед.
Частным случаям параллелепипеда является правильная призма - это призма, у которой все грани равны - куб.
Свойства прямой призмы
- Основания призмы равны
- Каждая из боковых граней обязательно является прямоугольником
- Боковые ребра призмы параллельны и равны между собой
- Боковые грани правильной призмы представляют собой равные прямоугольники
- При пересечении призмы и диагональной плоскости сечение представляет собой параллелограмм
- Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы
- Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах
- Перпендикулярное сечение перпендикулярно ко всем боковым граням
- Длина ребра прямой призмы равна ее высоте
Формулы прямой призмы
Где:
Ss - площадь боковой поверхности прямой призмы
Sb - площадь основания
V - объем прямой призмы
Vn - объем прямой призмы с правильным многоугольником в основании
Ssn - площадь боковой поверхности прямой призмы с правильным многоугольником в основании
P - периметр основания
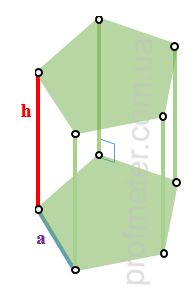
h - высота призмы, она же - длина бокового ребра прямой призмы
n - для прямой призмы, в основании которой лежит правильный многоугольник, количество сторон правильного многоугольника
a - для прямой призмы с правильным многоугольником в основании - длина стороны правильного многоугольника
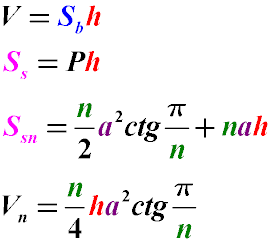
Площадь боковой поверхности призмы |
Описание курса
| Правильная четырехугольная призма
|

