Задачи на решение с помощью теоремы синусов

Примечание. Это часть урока с задачами по геометрии (раздел теорема синусов). Если Вам необходимо решить задачу по геометрии, которой здесь нет - пишите об этом в форуме. В задачах вместо символа "квадратный корень" применяется функция sqrt(), в которой sqrt - символ квадратного корня, а в скобках указано подкоренное выражение.

Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов, или, в расширенной формулировке:
Теорема синусов: Стороны треугольника (a,b,c) пропорциональны синусам противолежащих углов

Теорема синусов: Стороны треугольника (a,b,c) пропорциональны синусам противолежащих углов

где R - радиус описанной окружности

Теорию - формулировку и доказательство теоремы подробно см. в главе "Теорема синусов".

Задача. Найти сторону треугольника

В треугольнике XYZ угол Х=30 угол Z=15. Перпендикуляр YQ к ZY делит сторону ХZ на части XQ и QZ.
Найти XY, если QZ=1.5м

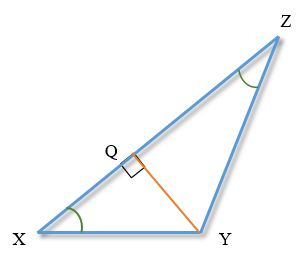
Произвольный треугольник с двумя острыми углами и высотой, опущенной из тупого угла на противоположную сторону

Произвольный треугольник с двумя острыми углами и высотой, опущенной из тупого угла на противоположную сторону

Решение.
Высота образовала два прямоугольных треугольника XYQ и ZYQ.
Для решения задачи воспользуемся теоремой синусов.

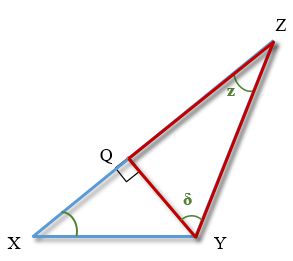
В результате того, что на одну из сторон была опущена высота, у нас образовался прямоугольный треугольник

В результате того, что на одну из сторон была опущена высота, у нас образовался прямоугольный треугольник

Для треугольника QYZ будет верным соотношение:
QZ / sin δ = QY / sin z

Поскольку прямоугольник QYZ прямоугольный, сумма углов любого треугольника равна 180 градусам, при этом
z = 15 градусов, то ∠δ = 180 - 90 - 15 = 75

Примем во внимание табличные значения некоторых тригонометрических функций:

синус 15 градусов равен sin( 15 ) =
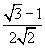
синус 75 градусов равен sin( 75 ) =

Решение задачи с помощью теоремы синусов - шаг за шагом. Этап 1

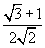
Пояснение к решению на картинке выше.

Записываем формулировку теоремы синусов на примере выбранного треугольника
Первая строка:
QZ / sin( 75 ) = QY / sin( 15 )

Вторая строка:
подставим значения синуса углов 75 и 15 градусов из таблицы
QZ / ( ( √3 + 1 ) / ( 2√2 ) ) = QY / ( ( √3 - 1 ) / ( 2√2 ) )

Третья строка - упрощаем выражение
QZ * 2√2 / ( √3 + 1 ) = QY * 2√2 / ( √3 - 1 )

В четвертой строке сокращаем левую и правую часть на 2√2
QZ / ( √3 + 1 ) = QY / ( √3 - 1 )

Пятая строка:
Учтем, что длина QZ нам известна и указана в условии задачи. Подставим ее в выражение
Теперь можно найти значение высоты QY
QY = 3/2 ( √3 - 1 ) / ( √3 + 1 )

Вторая часть решения.

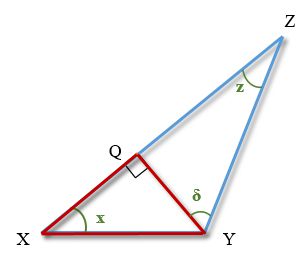
Вторая часть решения задачи на использование теоремы синусов. Выделяем второй треугольник относительно построенный высоты

Вторая часть решения задачи на использование теоремы синусов. Выделяем второй треугольник относительно построенный высоты

Поскольку длина высоты QY треугольника теперь известна, найдем величину XY с помощью теоремы синусов.

QY / sin( 30 ) = XY / sin( 90 )

Далее решаем аналогично первой части решения.

Примем во внимание табличные значения некоторых тригонометрических функций:

синус 30 градусов равен sin( 30 ) = 1 / 2
синус 90 градусов равен sin( 90 ) = 1

тогда

QY = XY sin ( 30 )
3/2 ( √3 - 1 ) / ( √3 + 1 ) = 1/2 XY
XY = 3 ( √3 - 1 ) / ( √3 + 1 ) ≈ 0.8 м

Ответ: 0,8 м или 3 ( √3 - 1 ) / ( √3 + 1 )

Теорема синусов | Описание курса | Теорема синусов (часть 2)