|
Примечание. Текст задачи взят с форума. Если Вы не нашли решения нужного типа задачи - пишите на форуме. Наверняка курс будет дополнен.
Задача.
|
Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если наклонные относятся между собой как 1:2, а проекции наклонных равны 1 см и 7 см.
|
З точки до плоскості проведені дві похилі. Знайдіть довжини похилих, якщо похилі відносяться між собою як 1:2, а проекції похилих рівні 1 см і 7 див.
|
Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .
Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
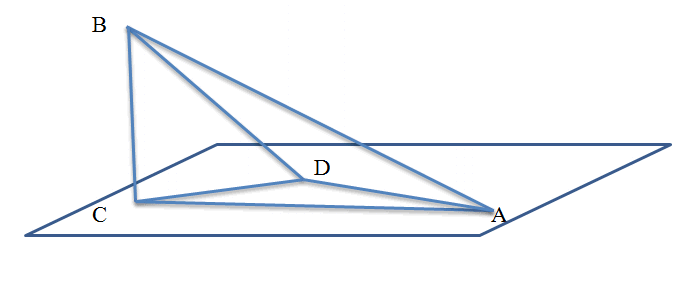
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора:
BC2 + AC2 = AB2
и
BC2 + CD2 = BD2
или
BC2 = AB2 - AC2
и
BC2 = BD2 - CD2
Теперь, учитывая, что левые части обоих выражений равны, получаем
AB2 - AC2 = BD2 - CD2
Подставим значения, которые известны по условию
AB2 - 72 = BD2 - 1
AB2 - 49 = BD2 - 1
Поскольку длины наклонных соотносятся как 1:2, обозначив длину BD как х (икс), получаем, что длина AB = 2x, откуда
4х2 - 49 = х2 - 1
3х2 = 48
х2 = 16
х = 4
Откуда длина второй наклонной равна 4 * 2 = 8 см
Ответ: 4 и 8 см.
Задача.
|
Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.
|

Решение.
Обозначим заданную в условии точку как В. Пусть наклонные к плоскости пересекают плоскость в точках А и D .
Опустим из точки В перпендикуляр на данную плоскость. Обозначим точку пересечения перпендикуляра с плоскостью как С.
Отметим, что у нас образовались прямоугольные треугольники DBC и ABC с прямым углом C. Из чего следует, что по теореме Пифагора: BC 2 + AC 2 = AB 2
и
BC2 + CD2 = BD2
или
BC2 = AB2 - AC2
и
BC2 = BD2 - CD2
Теперь, учитывая, что левые части обоих выражений равны, получаем
AB2 - AC2 = BD2 - CD2
Примем во внимание, что большая наклонная имеет большую проекцию.
Кроме того, поскольку одна наклонная на 26 см больше другой, то пусть BD = AB - 26.
Откуда AB = BD + 26
Подставим значения, которые известны по условию
(BD + 26)2 - 402 = BD2 - 122
BD2 + 52BD + 676 - 1600 = BD2 - 144
52BD = 780
BD = 15
Откуда AB = 15 + 26 = 41
Ответ: 41 и 15
Отрезок, пересекающий плоскость |
Описание курса
| Параллелограмм, рассеченный плоскостью
|

