Понятие многоугольника. Что такое многоугольник
Многоуго́льник — это геометрическая фигура, представляющая собой замкнутую ломаную линию.
Существуют три варианта определения многоугольников:
- Многоугольник - это плоская замкнутая ломаная линия;
- Многоугольник - это плоская замкнутая ломаная линия без самопересечений;
- Многоугольник - это часть плоскости, которая ограничена замкнутой ломаной.
Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Вершины многоугольника называются соседними, если они являются концами одной из его сторон.
Отрезки, соединяющие несоседние вершины многоугольника, называются диагоналями.
Углом (или внутренним углом) многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине, и находящийся во внутренней области многоугольника.
Внешним углом выпуклого многоугольника при данной вершине называется угол, смежный внутреннему углу многоугольника при этой вершине. В общем случае внешний угол это разность между 180° и внутренним углом
Многоугольник называют выпуклым, при условии, что одно из следующих условий является верным:
- Выпуклый многоугольник лежит по одну сторону от любой прямой, соединяющей его соседние вершины;
- Выпуклый многоугольник является пересечением нескольких полуплоскостей;
- Любой отрезок с концами в точках, принадлежащих выпуклому многоугольнику, полностью ему принадлежит.
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны, например равносторонний треугольник, квадрат и правильный пятиугольник.
Выпуклый многоугольник называется вписанным в окружность, если все его вершины лежат на одной окружности.
Выпуклый многоугольник называется описанным около окружности, если все его стороны касаются некоторой окружности.
Классификация (виды) многоугольников
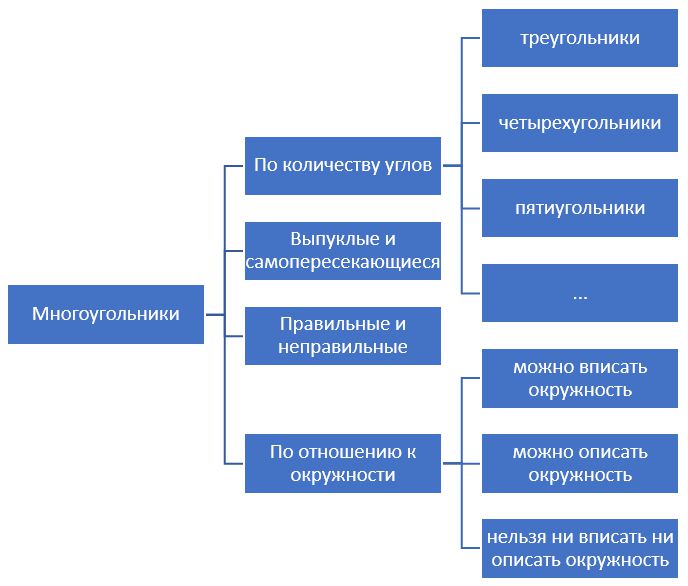
Классификация многоугольников по видам может быть по многим свойствам, самые главные из них:
- количество вершин
- выпуклость
- правильность
- возможность вписать или описать окружность
Многоугольник с тремя вершинами называется треугольником (см. треугольник), многоугольник с четырьмя вершинами называется четырехугольник (см. четырехугольник) и так далее по количеству вершин.
Выпуклый многоугольник лежит всегда по одну сторону от прямой, которая содержит любую из его сторон. (см. выше)
У правильного многоугольника равны все стороны и углы. Благодаря этому, они обладают некоторыми особыми свойствами (см. квадрат).
Самопересекающиеся многоугольники также могут быть правильными. Например, пентаграмма ("пятиконечная звезда").
Также многоугольники можно различать по отношению к возможности вписать в многоугольник или описать окружность около многоугольника. Могут быть многоугольники, вокруг которых нельзя описать окружность, а также вписать ее. Вместе с тем, вокруг любого треугольника всегда можно описать окружность.
Свойства многоугольника
- Сумма внутренних углов n-угольника равна (n − 2)π.
- Сумма внутренних углов правильного n-угольника равна 180(n − 2).
- Число диагоналей всякого многоугольника равно n(n − 3) / 2, где n — число сторон.
Далее - задачи о многоугольниках
Косинус двойного угла |
Описание курса
| Правильный многоугольник
|

