Объем призмы

Для нахождения объема призмы применяется общая универсальная формула:

V = Sh

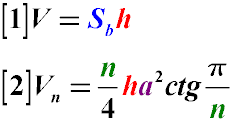
Универсальная формула нахождения объема любой призмы и универсальная формула нахождения объема любой правильной призмы (в основании которой лежит правильный многоугольник)

Универсальная формула нахождения объема любой призмы и универсальная формула нахождения объема любой правильной призмы (в основании которой лежит правильный многоугольник)

где:

V - объем призмы
Vn - объем призмы, в основании которой лежит правильный многоугольник с n сторонами
Sb - площадь основания призмы
h - высота призмы
n - количество сторон правильного многоугольника, который лежит в основании призмы
a - длина стороны правильного многоугольника

Как найти объем треугольной призмы (с треугольником в основании)

Если в основании призмы лежит треугольник, то для нахождения ее объема можно применить формулы нахождения площади треугольника и умножить полученное значение на высоту призмы.
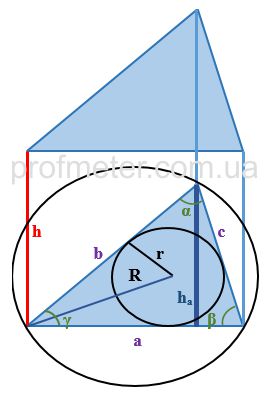
Треугольная призма с отмеченными на рисунке сторонами основания описанной и вписанной окружностью и высотой основания

Треугольная призма с отмеченными на рисунке сторонами основания описанной и вписанной окружностью и высотой основания

Формулы нахождения объема призмы, в основании которой лежит произвольный треугольник через его стороны, углы, радиус вписанной и описанной окружности

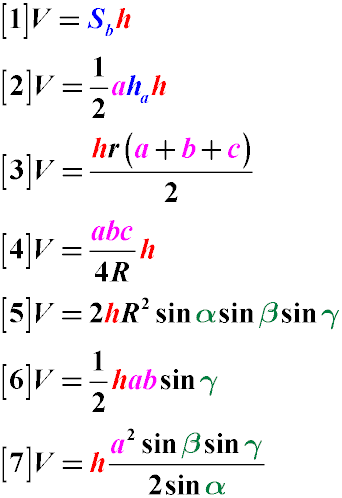
Объем треугольной призмы можно найти через высоту основания h_a и сторону a, на которую эта высота опущена (Формула 2). Не путайте h_a и h.
Объем треугольной призмы можно найти через радиус вписанной окружности r и сумму длин сторон основания (a,b,c).(Формула 3)
Объем треугольной призмы можно вычислить как произведение длин сторон основания на четыре радиуса описанной окружности R, умноженное на высоту призмы. (Формула 4)
Также, зная радиус описанной окружности, объем треугольной призмы можно найти как произведение синусов всех углов основания на квадрат радиуса описанной окружности, умноженное на удвоенную высоту призмы (Формула 5).
Если известен угол между двумя сторонами основания и сами эти стороны, то половина произведения сторон основания на синус угла между ними и на высоту призмы, также позволит вычислить ее объем (Формула 6).

Есть также формулы нахождения объема призмы для специальных случаев, когда в основании лежит геометрическая фигура с "особенностями". Например, если в основании прямой призмы лежит равносторонний, прямоугольный или равнобедренный треугольник, тогда количество формул, которыми можно воспользоваться для расчета объем призмы, существенно расширяется:

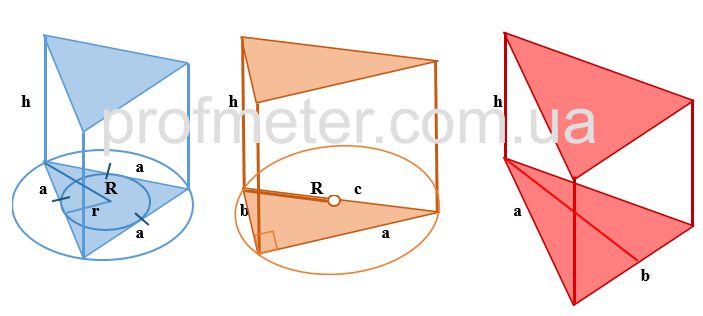
Прямые призмы, в основании которых лежит треугольник - правильный (равносторонний), прямоугольный, равнобедренный с обозначениями размеров сторон, вписанными и описанными окружностями

Прямые призмы, в основании которых лежит треугольник - правильный (равносторонний), прямоугольный, равнобедренный с обозначениями размеров сторон, вписанными и описанными окружностями

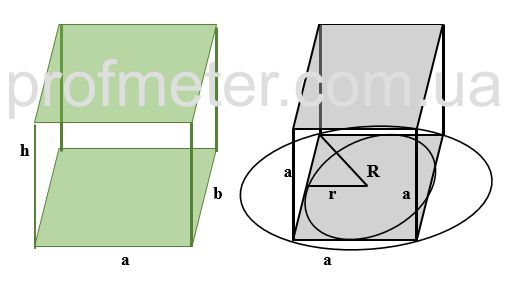
Объем правильной треугольной призмы (с правильным треугольником в основании)

На рисунке выше правильная треугольная призма изображена синим цветом.

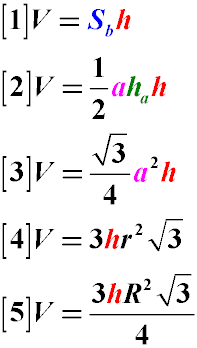
Формула объема призмы с правильным треугольником в основании для нахождения его через стороны, радиус вписанной и описанной окружности через высоту

Формула объема призмы с правильным треугольником в основании для нахождения его через стороны, радиус вписанной и описанной окружности через высоту

Где:
V - объем правильной треугольной призмы
h_a - высота основания, опущенная на сторону основания a
h - высота призмы
r - радиус вписанной в основание окружности
R - радиус окружности, описанной вокруг основания правильной треугольной призмы

Объем призмы с прямоугольным треугольником в основании

Призма с прямоугольным треугольником в основании, с отмеченными сторонами, углами, вписанной и описанной окружностями

Формулы вычисления объема призмы с прямоугольным треугольником в основании. Исходя из длин сторон прямоугольного треугольника, его углов, радиусов вписанной или описанной окружности

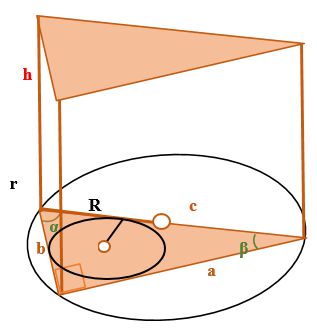
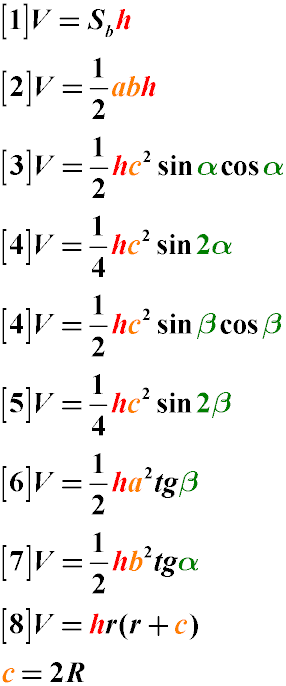
Где:
V - объем призмы с прямоугольным треугольником в основании
h - высота призмы
α - угол основания, противолежащий стороне a (катету a) прямоугольного треугольника
β - угол основания, противолежащий стороне b (катету b) прямоугольного треугольника
a,b - катеты прямоугольного треугольника, который является основанием призмы
c - гипотенуза прямоугольного треугольника, который является основанием призмы
r - радиус вписанной в основание призмы окружности
R - радиус описанной вокруг основания призмы, которое является прямоугольным треугольником, окружности

Учтите, что если, вокруг прямоугольного треугольника описана окружность, то гипотенуза треугольника лежит на ее диаметре, то есть c = 2R. Поэтому, при необходимости, можно заменить в формулах c на (2R).

Объем призмы с равнобедренным треугольником в основании

Призма с равнобедренным треугольником в основании с обозначенными высотой равнобедренного треугольника, сторонами и углами

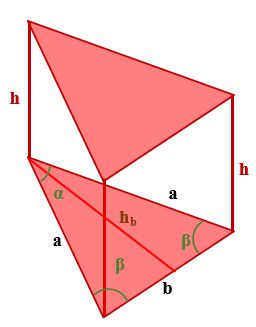
Если в основании призмы лежит равнобедренный треугольник, для нахождения ее объема можно воспользоваться следующими формулами:
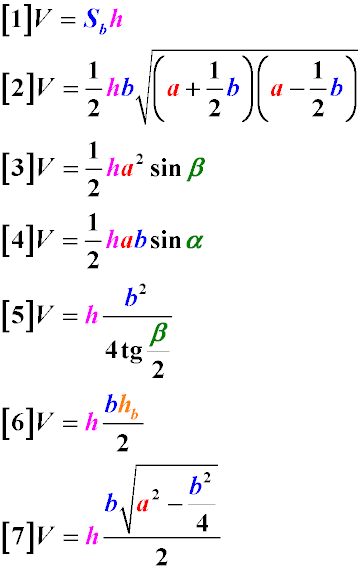
Формулы нахождения объема призмы с равнобедренным треугольником в основании

Формулы нахождения объема призмы с равнобедренным треугольником в основании

где:
V- объем призмы с равнобедренным треугольником в основании
h - высота призмы
h_b - высота равнобедренного треугольника, опущенная на его основание
a - длина одной из равных сторон равнобедренного треугольника, лежащего в основании призмы
b - основание равнобедренного треугольника
α - угол между сторонами и основанием равнобедренного треугольника
β - угол между равными сторонами равнобедренного треугольника, который лежит в основании призмы

Объем параллелепипеда и куба

Если в основании прямой призмы лежит прямоугольник, то количество формул для нахождения объема такой призмы также будет больше:
Прямые четырехугольные призмы, в основании которых лежит четырехугольник - параллелепипед и куб с обозначенными размерами сторон

Прямые четырехугольные призмы, в основании которых лежит четырехугольник - параллелепипед и куб с обозначенными размерами сторон

Формулы нахождения объема параллелепипеда и куба, в том числе через радиус вписанной и описанной окружности

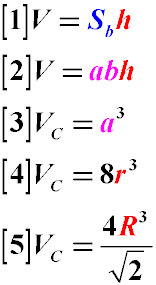
где:
V - объем призмы, в основании которой лежит прямоугольник
Vc - объем куба
h - высота призмы
a - длина стороны основания
b - длина второй стороны основания
R - радиус окружности, описанной вокруг основания куба
r - радиус окружности, вписанной в основание куба

Призма. Параллелепипед. Куб. Решение задач | Описание курса | Площадь боковой поверхности призмы