Задача.
Расстояние от точки О до сторон квадрата равно 13 см. Найдите расстояние от точки О до плоскости квадрата, если сторона квадрата равна 10 см.

Решение.

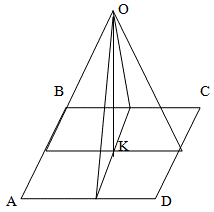
Точка О, которая равноудалена от каждой из сторон квадрата будет проецироваться в точку пересечения его диагоналей (центр). Докажем это.

Опустим из точки О на плоскость квадрата перпендикуляр, который коснется плоскости квадрата в точке К. Теперь докажем равенство образовавшихся прямоугольных треугольников треугольников. Поскольку их гипотенузы равны по условию задачи, а один из катетов - общий, то вторые катеты также равны как следствие из теоремы Пифагора. Таким образом, точка К равноудалена от сторон квадрата и является его центром.

Поскольку сторона квадрата равна 10 см, то точка К удалена от каждой из них на 10/2 = 5 см . Из имеющегося прямоугольного треугольника с катетом 5 см и гипотенузой 13 см, найдем его катет (который и является расстоянием от точки О до плоскости квадрата. 

OK ² = 13² - 5 ²
OK = 12

Ответ: 12 см